ответ: 180.
Вот формула площади трапеции:
, где a и b - основания трапеции, а h - высота (S, разумеется, площадь).
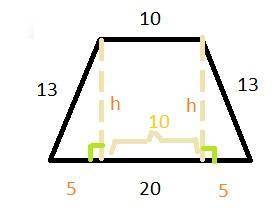
Вот только одна проблема: мы не знаем высоты. Но чтобы ее узнать, можно отсечь от трапеции (например, справа) прямоугольный треугольник. Его гипотенуза (c)- это боковая сторона трапеции, которая равна 13. Нижний катет (b) будет равен 
. Почему - можно увидеть на рисунке ниже. Второй катет этого треугольника (а) - это и есть высота, которую можно найти по теореме Пифагора:
Теперь высоту мы знаем и можем найти площадь трапеции:
Задача решена!
2f(x), а, значит, и функция f(x).
Пошаговое объяснение:
Мы воспользуемся следующими свойствами непрерывных функций:
(1) сумма и разность непрерывных функций — непрерывные функции;
(2) если g(x) — непрерывная функция, функция g(ax) также непрерывна.
Теперь заметим, что по условию непрерывны функции f(x) + f(2x) и f(x) + f(4x), а в силу свойства (2) вместе с функцией f(x) + f(2x) непрерывна и функция f(2x) + f(4x).
Далее, по свойству (1) непрерывна функция (f(x) + f(2x)) + (f(x) + f(4x)) – (f(2x) + f(4x)) = 2f(x), а, значит, и функция f(x).
второе число = 1 + первое число
примем первое число за X
X * 2/3 + ( X + (X+1))/2 = 20,5
X * 2/3 + ( 2X + 1 ) / 2 = 20,5
X * 2/3 + X + 0,5 = 20,5
5/3 X = 20
X = 20 * 3/5
X = 12
вторео число 13