Треугольник — это геометрическая фигура, образованная в результате соединения трех точек, не лежащих на одной прямой. Проще говоря, это просто фигура, имеющая три стороны.
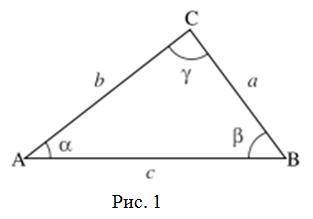
На рисунке 1 изображен треугольник со сторонами a, b, c и углами α, β, γ.
Вершинами треугольника являются точки A, B, C.
Периметр треугольника измеряется путем сложения трех его сторон:
Р= a+b+c, где Р- периметр, a, b и с — стороны.
Равносторонним называется треугольник, у которого все стороны равны (a=b=c). Все углы в таком треугольнике равняются 60°.
Третий признак равенства треугольников звучит так:
Если три стороны одного треугольника равны соответственно трем сторонам второго треугольника, то такие треугольники равны.
История математических обозначений — история разработки символов, используемых для компактной записи математических уравнений и формул. Помимо индо-арабских цифр и букв различных алфавитов (латинского, в том числе в готическом начертании, греческого и еврейского), математический язык использует множество специальных символов, изобретённых за последние несколько столетий.
Хорошо продуманные обозначения, отражающие свойства изучаемых объектов избежать ошибок или неправильной трактовки, переносят часть исследования на технический уровень, нередко «подсказывают» правильный путь к решению задачи. По словам Альфреда Уайтхеда, удачное обозначение освобождает мозг от ненужной работы, тем самым позволяя ему сосредоточиться на более важных задачах[1].
Первоначально (например, в «Началах» Евклида) математические утверждения формулировались словесно. Такая запись была громоздкой, часто неоднозначной, а алгебраические преобразования требовали незаурядной квалификации. Большой вклад в развитие обозначений внёс Франсуа Виет (XVI век); в частности, он начал использовать буквенные обозначения вместо конкретных чисел. Постепенно практически все слова в математических формулах (обозначения операций, отношений сравнения и т. д.) были заменены специальными символами — математика обрела собственный язык, не требующий перевода, язык с чётко определённым смыслом «слов» и строгой грамматикой, позволяющий выводить из истинных утверждений другие, столь же истинные.