Находим абсциссы точек пересечения прямых с осью Ох.
x-2y+4=0, y=0, х = -4.
y=2x+3, y=0, х = -3/2 = -1,5.
Теперь определяем точку пересечения прямых.
Первую прямую выразим относительно у =(1/2)х + 2
(1/2)х+2=2x+3,
1,5х = -1,
х = -2/3.
Теперь можно переходить к площади.
Заданная фигура состоит из двух частей.
Первая S1 - ограничена прямой у = (1/2)х + 2, осью Ох и двумя прямыми х = -4, х = -1,5.
Вторая S2- заключена между наклонными прямыми и прямыми х = 1,5 и х = -2/3.
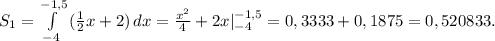
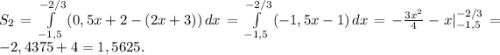
Получаем ответ: S = 0,520833+1,5625 = 2,083333 = 25/12.
этот результат легко проверить:
S = (1/2)*2.5*(5/3) = 25/12.
Здесь (5/3) - ордината точки пересечения прямых.
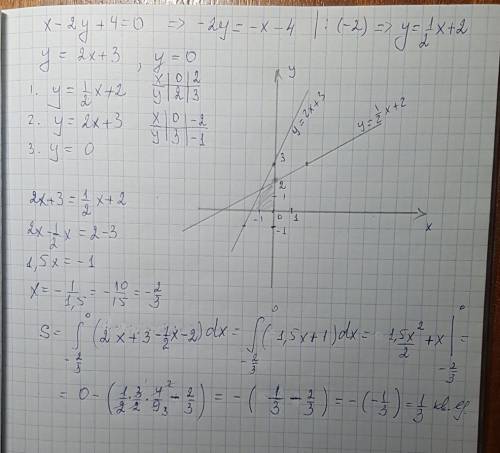
Находим абсциссы точек пересечения прямых с осью Ох.
x-2y+4=0, y=0, х = -4.
y=2x+3, y=0, х = -3/2 = -1,5.
Теперь определяем точку пересечения прямых.
Первую прямую выразим относительно у =(1/2)х + 2
(1/2)х+2=2x+3,
1,5х = -1,
х = -2/3.
Теперь можно переходить к площади.
Заданная фигура состоит из двух частей.
Первая S1 - ограничена прямой у = (1/2)х + 2, осью Ох и двумя прямыми х = -4, х = -1,5.
Вторая S2- заключена между наклонными прямыми и прямыми х = 1,5 и х = -2/3.
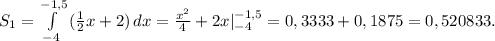
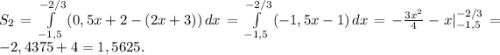
Получаем ответ: S = 0,520833+1,5625 = 2,083333 = 25/12.
этот результат легко проверить:
S = (1/2)*2.5*(5/3) = 25/12.
Здесь (5/3) - ордината точки пересечения прямых.

НОД (56; 72) = 8.
Как найти наибольший общий делитель для 56 и 72
Разложим на простые множители 56
56 = 2 • 2 • 2 • 7
Разложим на простые множители 72
72 = 2 • 2 • 2 • 3 • 3
Выберем одинаковые простые множители в обоих числах.
2 , 2 , 2
Находим произведение одинаковых простых множителей и записываем ответ
НОД (56; 72) = 2 • 2 • 2 = 8
Пошаговое объяснение: