вот держи думаю что правильно. деятель бунин.
бунин иван алексеевич (1870-1953). писатель. из обедневшей дворянской семьи. в молодости работал корректором, статистиком, библиотекарем, репортером. печатался с 1887 г.
первые книги и. бунина - стихотворные сборники. стихи его - пример «старой» классической формы. тема поэзии молодого бунина - родная природа. тогда же он начал писать рассказы. в 1899 г. и. бунин начинает сотрудничать с издательством «знание». лучшие рассказы этого периода - «антоновские яблоки» (1900), «сосны» (1901), «чернозем» (1904). серьезный общественный резонанс имела повесть «деревня» (1910). хроникой вырождения усадебного дворянства стала повесть «суходол» (1911). проза и. бунина - образец живописности, строгости, ритмической выразительности.
поэтический сборник и. бунина «листопад» (1901 г.) - получил пушкинскую премию. в 1909 г. бунин избирается почетным академиком. прославился перевод буниным поэмы лонгфелло «песня о гайавате». в 1920 г. бунин эмигрирует. в дальнейшем он живет и работает во франции.
в эмиграции он создает произведения о любви («митина любовь», 1925 г.; «дело корнета елагина», 1927 г.; цикл новелл «темные аллеи» 1943 центральное место в творчестве позднего бунина занимает автобиографический роман «жизнь арсеньева» (1930 в 1933 г. писателю была присуждена нобелевская премия. за рубежом и. бунин создал также философско- трактат о толстой л.н.л.н. толстом «освобождение толстого» (1937 г.) и «воспоминания» (1950
очевидно при n = 1 не существует графа с 2 ребрами, поэтому n ≥ 2
степень вершины - количество всех ребер, выходящих из вершины deg(v)
сумма степеней всех вершин равна удвоенному количеству всех ребер
т.е. в данном графе сумма степеней вершин
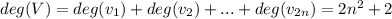
будем доказывать от противного. предположим такого ребра нет.
рассмотрим любые 4 вершины, чтобы среди них не было ребра, которое принадлежит двум циклам длины 3, среди них может быть проведено не более 4 ребер, как бы не проводили пятое, всегда оно дополнит второй цикл.
поэтому сумма степеней всех вершин среди любых четырех не превосходит 4*2 = 8
рассмотрим четверки:
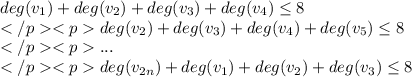
сложим все неравенства и получим, что
4*deg(V) ≤ 16n
deg(V) ≤ 4n
но deg(V) по условию равно 2n² + 2
2n² + 2 ≤ 4n
2(n-1)² ≤ 0
неравенство может выполниться только при n = 1, но как уже было отмечено, этот случай не удовлетворяет по условию.
Значит, наше предположение было не верно.
ответ: доказано.
192-84=108 трехэтажные
можно другим
16/16-7/16=9/16
192:16*9=108