1. Пусть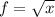 
, 
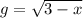. Заметим, что 
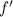и 
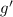монотонно убывают, значит, 
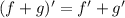функция монотонная, следовательно, имеет не более одного корня. Из этого следует, что у уравнения 
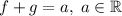не более двух корней.
2. Заметим, что если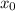 
является решением, то 
тоже. Очевидно, что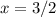 
является осью симметрии (причем единственной) графика 
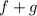. Иначе говоря, пара 
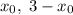исчерпывает все решения указанного уравнения, если таковые имеются. Значит, достаточно потребовать, чтобы 
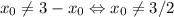. Итак, 
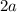пробегает область значения рассматриваемой функции, кроме того 
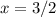, которому соответствует (это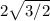 
).
3. Функция непрерывна, поэтому достаточно посмотреть на наименьшее и наибольшее значения. Наименьшее значение достигается в 0 (то есть значение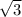 
, а наибольшее в 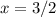. Получаем ответ: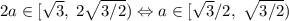 
ответ:
пошаговое объяснение:
число выпадения гербов подчинено биномиальному закону с параметрами n=6, p=q=0,5.
вероятность выпадения герба k < 6 раз вычисляется по формуле бернулли
p(k)=(с из 6 по k)•p^k•q^(n-k).
менее двух раз это ноль или один раз, поэтому
p(k < 2)=p(0)+p(1).
p(0)= (с из 6 по 0)•0,5^6=0,015625;
p(1)= (с из 6 по 1)•0,5^6=6•0,015625= 0,09375.
p(k < 2)=p(0)+p(1)= 0,109375.
не менее двух раз это противоположное событие тому, что герб выпадет менее двух раз, поэтому
p(k > = 2)=1-p(k < 2)=1-0,109375=0,890625.