∠АВН = 30°; ∠ВАР = 45°.
Пошаговое объяснение:
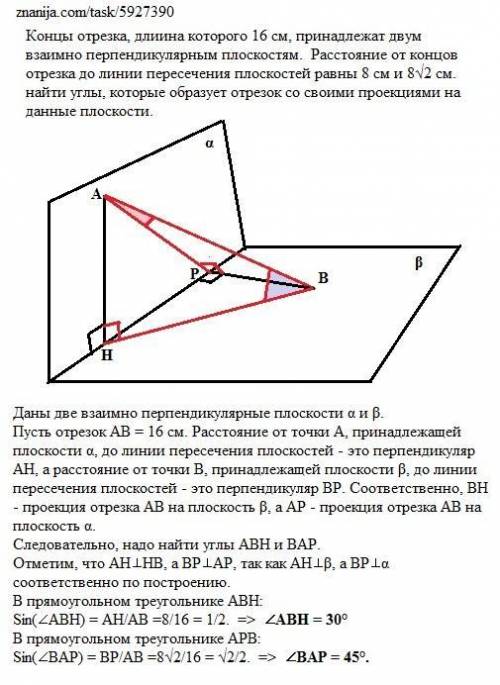
Концы отрезка, длина которого 16 см, принадлежат двум взаимно перпендикулярным плоскостям. Расстояние от концов отрезка до линии пересечения плоскостей равны 8 см и 8√2 см. найти углы, которые образует отрезок со своими проекциями на данные плоскости.
Решение.
Даны две взаимно перпендикулярные плоскости α и β.
Пусть отрезок АВ = 16 см. Расстояние от точки А, принадлежащей плоскости α, до линии пересечения плоскостей - это перпендикуляр АН, а расстояние от точки В, принадлежащей плоскости β, до линии пересечения плоскостей - это перпендикуляр ВР. Соответственно, ВН - проекция отрезка АВ на плоскость β, а АР - проекция отрезка АВ на плоскость α.
Следовательно, надо найти углы АВН и ВАР.
Отметим, что АН⊥НВ, а ВР⊥АР, так как АН⊥β, а ВР⊥α соответственно по построению.
В прямоугольном треугольнике АВН:
Sin(∠АВН) = АН/АВ =8/16 = 1/2. => ∠АВН = 30°
В прямоугольном треугольнике АРВ:
Sin(∠ВАР) = ВР/АВ =8√2/16 = √2/2. => ∠ВАР = 45°.
1) Так как по усл в тр АВС уг С- тупой, то основание высоты из вершины этого угла N лежит на стороне АВ ; эта сторона АВ - основание р/б тр АВС
2) Высота CN в тр АВС является медианой этого тр по св-ву р/б тр => AN = NB
3) Рассм тр АСN: Р(ACN) = 22 см ; Р(АСN) = AC+AN + CN, CN = 6 см,=>
AC + AN = 22-6 = 16 см, но АС = СВ (из усл), AN = NB (из 2), =>
Р(АСВ) = АС + СВ + АВ = АС + СВ + AN+NB = 2AC + 2 AN = 2(AC + AN);
P(ACB) = 2*16 = 32 см