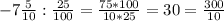Представьте в виде a/n(где а-целое, а n-натуральное число): а)сумму -2/9+5/18 и сумму 3,9-4,7; б)произведение -22/7*1(целую) 3/11 и произведение -5,6*(-1,2); в)часное -7,5: (-0,25) и часное -0,8: (-0,6).
Произведение двух наибольших = 225 Чтобы получить 225, можно перемножить такие разные натуральные числа: 225*1, 75*3, 45*5, 25*9.
Произведение двух наименьших = 16 Чтобы получить 16, можно перемножить такие разные натуральные числа: 16*1, 8*2.
Т.к. есть 2 самых меньших и 2 самых больших, то меньшие не могут быть больше больших (очевидно же). Поэтому есть лишь вариант 25,9 и 8,2. В любых других случаях одно из больших чисел меньше одного из меньших чисел, чего не может быть. Сумма всех чисел = 25+9+8+2 = 44
1) на отрезке [0;3] функция y=x³-4 возрастает, поэтому наименьшее значение она принимает при x=0, и оно равно 0-4=-4, а наибольшее - при x=3, и оно равно 3³-4=23.
2) перепишем функцию в виде y=-3x-1. Эта функция убывает на всей числовой оси, поэтому Ymax=y(-2)=5 и Ymin=y(0)=-1.
3) Функция убывает на промежутке [π/3;π/2) и возрастает на промежутке (π/2;5*π/6]. При этом y(π/3)=1-√3<y(5*π/6)=0, поэтому Ymax=y(5*π/6)=0, а Ymin=y(π/2)=-1
4) На промежутке [0;π/2] функция y=1+sin(x), а вместе с ней и функция y1=√(1+sin(x)) возрастают. Поэтому Ymin=y1(0)=1, а Ymax=y1(π/2)=√(1+1)=√2
а)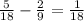
б)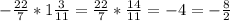
в)