(3.3-1.8)*3 целых 5/9-дроби=(1,5)*(3*9+5)/9-дроби=15/10*32/9-дроби=(3*5)/(2*5)*(2*16)/(3*3)-дроби=16/3-дроби=
(что за дроби?)
(2целых 1/12-1 целая 3/4)*1.25=(25/12-7/4)*125/100=(25/12-21/12)*5/4=4/12*5/4=5/12
3 целых 5/18:59/60+2.6=(3*18+5)/18:59/60+26/10=59/18:59/60+13/5=(59*60)/(18*59)+13/5=60/18+13/5=10/3+13/5=(5*10+3*13)/15=89/15=5 целых 14/15
2.25*0.8-3/8=1,8-0,375=1,425 или 1 целая 425/1000=1 целая 17/40
(3/4+1 целая7/8):0.25=(3/4+15/8):0,25=(6/8+15/8):0,25=21/8:1/4=21*4/8=21/2=10 целых 1/2 или 10,5
1) S=ab=400м*1250м=50 000 м2 = 50 га (1га =10 000м2)
2) V=abc=3м*8м*5дм=30дм*80дм*5 дм = 12 000 дм3 = 12 м3
3)
а)V=S/T=36 км / 4 ч =9км/ч
б) S=V*T=650км/ч*2ч=1300 км
в) T=S/V=40 км / 10км/ч=4 ч
5) 1) 16*4=64 см2 - площадь прямоугольника и квадрат
2) нам нужно найти такое число, которое в квадрате даст 64. это число 8, значит сторона квадрата 8 см (т.к. площадь квадрата сторону умнож. на саму себя)
6)
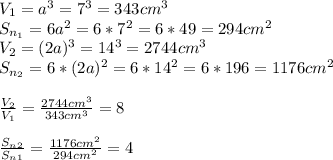
первый объем 343, второй 2744, площадь первой пов-ти 296, второй 1184, объем в 8 раз, площади в 4
7)
1) 54:6=9 см2 - площадь одной грани
2) нужно найти число, кторое в квадрате дает 9. это число 4. значит 3 - ребро куба
3) V=a^3=3^3=3*3*3=27 m3
Число игр, в которых участвовала команда, в любой момент находится в пределах от 0 до N-1. При этом не может так оказаться, что одна команда сыграла 0 матчей, а какая-то сыграла все N-1. Значит, всегда есть повторения, что является сюжетом известной задачи.
Рассмотрим N-1 команду кроме A. Число игр изменяется в тех же пределах, и значения 0 и N-1 по-прежнему несовместимы. Если все значения разные, то это или от 0 до N-2 включительно, либо от 1 до N-1.
В первом случае есть команда, которая ни с кем не играла. Если её исключить из рассмотрения, то кроме A останется N-2 команды со значениями от 1 до N-2. Тогда последняя из них играла со всеми, включая A. Если и эту команду исключить из рассмотрения, то помимо A останется N-3 команды со значениями от 0 до N-4, и с ними A играла 12 раз. Далее через два шага мы получим N-5 команд со значениями от 0 до N-6, с которыми A играла 11 раз, и так далее.
Получается, что при значениях игр команд от 0 до N-2k, команда A с ними провела 14-k встреч. Так мы дойдём до k=13, и окажется, что A играла одну встречу с N-25 командами, у которых значения лежат в пределах от 0 до N-26 включительно. Отсюда следует, что N=27 или N=28. Сами эти значения подходят, так как данная процедура может быть проделана в обратном порядке с получением расписания. При N>28 следующий шаг даёт противоречие: если команда A не играла ни с кем из оставшихся, то там не могло получиться попарно различных значений, если остались по крайней мере двое.
Во втором случае, при значениях от 1 до N-1, есть команда, игравшая со всеми. Тогда её, как и выше, исключаем. Получается, что A провела 12 встреч с командами, у которых количество игр принимает значения от 0 до N-3 (значение N-1 исчезло, а остальные уменьшились на 1). Видно, что при уменьшении на единицу числа игр A, правая граница значений для остальных команд уменьшается на 2. Значит, при уменьшении числа игр A ещё на 11 (оно станет равным 1), получатся границы от 0 до N-25, откуда следует, что N=26 или N=27, причём эти значения подходят.
Таким образом, в турнире могло участвовать 26, 27 или 28 команд; сумма этих значений равна 81