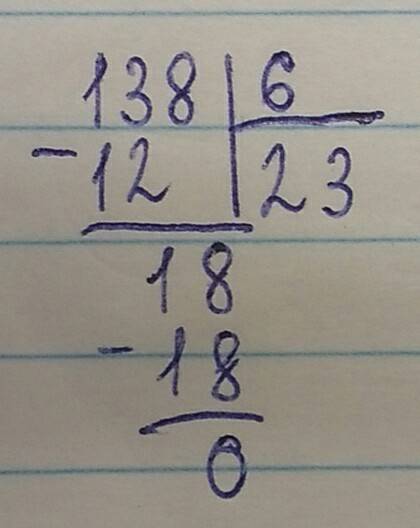
№1. 3
№2. 12
Пошаговое объяснение:№1.
Обозначим точки:
х-первая
у-вторая
с-третья
Составим всевозможные варианты соединения:
хус, хсу, ухс, усх, сху, сух
Ломанные:
хус и сух
хсу и усх
сху и ухс
Одинаковые, просто они читаются наоборот⇒берём по одному названию ломанной из каждой строчки:
хус
хсу
сху
Значит можно нарисовать 3 разных ломаных из двух звеньев с вершинами в этих точках.
№2.
Решается аналогично предыдущей задаче.
Обозначим точки:
х-первая
у-вторая
с-третья
m-четвёртая
Всевозможные варианты:
Т.к точек 4, и повторяться они не должны,то
4!=1*2*3*4=6*4=24 варианта
Но, среди этих 24 вариантов тоже есть одинаковые, они также читаются наоборот.
Одинаковых ровно половина, значит у нас остаётся 12 вариантов ломанных из двух звеньев с вершинами в этих точках можно нарисовать.
Из исходного равенства видно, что p>q, в противном случае равенство не выполнялось бы. Предположим, что p=q+k, где k - натуральное. Тогда 2q+k=(q+k-q)^3, отсюда 2q+k=k^3 или 2q=k^3-k=k(k^2-1). Тогда q=k(k^2-1)/2. Отсюда сразу видно, что q будет простым только при k=2, поскольку при k=1 получаем 0, а при k>2 будем получать составные числа, а по условию q простое. Итак, при k=2, q=2*(2^2-1)/2=3. Тогда p=q+k=3+2=5. Это единственное решение удовлетворяющее данному равенству.
ответ: p=5, q=3.