45° и 135°
Пошаговое объяснение:
Для начала вспомним, что такое смежные углы и их "функции". Смежные углы это два и более углов, у которых есть общие стороны (более точное определение все же прочитайте в учебнике, я уже не помню(, а также они по определению вместе составляют 180°. На основе этой информации мы можем составить уравнение, например:
1 угол x° (так как при составлении уравнения важно обозначить наименьшее значение; в качестве наименьшего значения и корня самого уравнения возьмем 1-ый угол)
2 угол (x+90)° (по условию задачи нам известно, что 2-ой угол больше 1-ого на 90°)
Составим уравнение на основе определения смежных углов и решим его:
x + ( x + 90 ) = 180 (так как мы знаем, что в сумме они все равно составят 180°)
2x + 90 = 180
2x = 180 - 90
2x = 90
x = 45
Следовательно 1-ый угол равен 45°, а 2-ой равен 45+90=135°
Для проверки сложите значение первого и второго угла, получается 180, значит задача решена верно
По условию задания составим уравнение расстояния произвольной точки М(х; у) от точки P(1; -1) в 2 раза меньшего, чем от точки М до прямой х = 4.
√((x-1)² + (y + 1)²) = |4 - x)|/2.
Модуль в правой части взят, чтобы длина не была отрицательной для точек, расположенных левее оси Оу.
Возведём обе части в квадрат.
x² - 2x + 1 + (y + 1)² = (16 - 8x + x²)/4,
4x² - 8x + 4 + 4(y + 1)² = 16 - 8x + x²,
Приведём подобные: 3x² + 4(y + 1)² = 12.
Разделим обе части на 12.
(3x²/12) + (4(y + 1)²)/12 = 1. Приведём к каноническому виду.
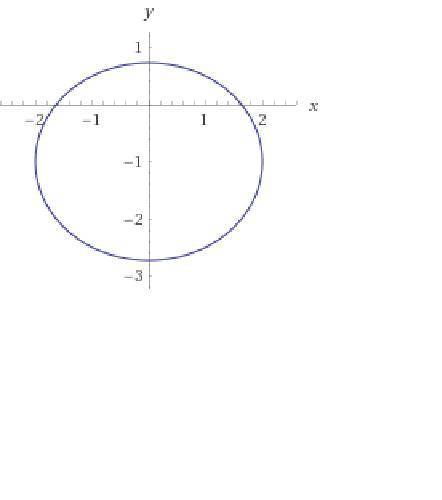
(x²/2²) + ((y + 1)²)/(√3)²) = 1.
Получено искомое уравнение. Это уравнение эллипса.
Центр её расположен в точке (0; -15).
Полуоси: действительная равна а =2, мнимая b = √3.
Найдем координаты ее фокусов: F1(-c;0) и F2(c;0), где c - половина расстояния между фокусами
Определим параметр c: c² = a² - b² = 4 - 3 = 1 .
c = √1 = 1.
Тогда эксцентриситет будет равен: е = с/а = 1/2 .
((4х-4+3)/4)*(2/3)=0
((4х-1)*2)/(3*4)=0 - 2 уйдет а 4 заменится на 2
(4х-1)/(3*2)=0
(4х-1)/6=0 домножим все уравнение на 6
4х-1=0
х=1/4
х=0,25
ответ: 1/4 или 0,25(если проходили такие дроби)