Математика: Исследуйте функцию y=x-4 на непрерывность

Исследуйте функцию y=x-4 на непрерывность

👇

Ответ:

andrewbukharin2

14.05.2021

Y=x-4
D(y)∈R
Функция определена на множестве действительных чисел.
y`=1
y`>0 значит на всей области непрерывная функция возрастает

4,6(51 оценок)

Открыть все ответы

Ответ:

kantuz

14.05.2021

Начнем строить цепочку.

Удобно начать с числа 16, так как это наибольшее число. Даже если рядом с ним поставить число 15, то их сумма даст 31, а значит все потенциальные квадраты должны быть не больше 31.

Итак, от 16 до 31 есть только один квадрат: 25. Значит, дополняем число 16 до 25 числом 9:

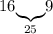
$16 \underset{25}{\underbrace{}} 9$

Число 9 до 25 мы только что дополняли, значит остается только дополнить его до 16 - числом 7:

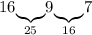
$16 \underset{25}{\underbrace{}} 9\underset{16}{\underbrace{}}7$

Число 7 до 25 дополнить не можем (числа 18 среди карточек нет), значит остается дополнить его до 9 - числом 2:

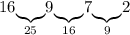
$16 \underset{25}{\underbrace{}} 9\underset{16}{\underbrace{}}7\underset{9}{\underbrace{}}2$

Число 2: до 4 дополнить не можем, так как нужное в этом случае число 2 занято, до 9 дополняли только что, остается дополнить его до 16 - числом 14:

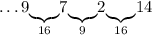
$\ldots9\underset{16}{\underbrace{}}7\underset{9}{\underbrace{}}2\underset{16}{\underbrace{}}14$

Число 14: до 16 дополнить не можем, так как нужное в этом случае число 2 занято, остается дополнить его до 25 - числом 11:

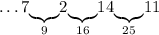
$\ldots7\underset{9}{\underbrace{}}2\underset{16}{\underbrace{}}14\underset{25}{\underbrace{}}11$

Число 11: можем дополнить только до 16 - числом 5:

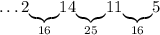
$\ldots2\underset{16}{\underbrace{}}14\underset{25}{\underbrace{}}11\underset{16}{\underbrace{}}5$

Число 5: можем дополнить только до 9 - числом 4:

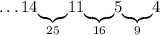
$\ldots14\underset{25}{\underbrace{}}11\underset{16}{\underbrace{}}5\underset{9}{\underbrace{}}4$

Число 4: можем дополнить только до 16 - числом 12:

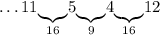
$\ldots11\underset{16}{\underbrace{}}5\underset{9}{\underbrace{}}4\underset{16}{\underbrace{}}12$

Число 12: можем дополнить только до 25 - числом 13:

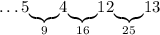
$\ldots5\underset{9}{\underbrace{}}4\underset{16}{\underbrace{}}12\underset{25}{\underbrace{}}13$

Число 13: можем дополнить только до 16 - числом 3:

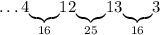
$\ldots4\underset{16}{\underbrace{}}12\underset{25}{\underbrace{}}13\underset{16}{\underbrace{}}3$

Число 3. Только на этом шаге возникает несколько вариантов. Мы можем дополнить его до 4 или до 9. Пробуем дополнить до 4 - числом 1:

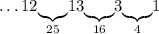
$\ldots12\underset{25}{\underbrace{}}13\underset{16}{\underbrace{}}3\underset{4}{\underbrace{}}1$

Число 1. Опять же, мы можем дополнить его до 9 или до 16. Пробуем дополнить до 9 - числом 8:

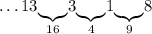
$\ldots13\underset{16}{\underbrace{}}3\underset{4}{\underbrace{}}1\underset{9}{\underbrace{}}8$

Число 8. До 9 его мы дополняли только что, до 16 дополнить его не можем (отсутствует еще одна восьмерка), до 25 также дополнить не можем (карточки 17 у нас нет). Тупик.

Значит, нужно вернуться назад и попробовать дополнить число 1 до 16 - числом 15:

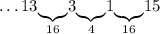
$\ldots13\underset{16}{\underbrace{}}3\underset{4}{\underbrace{}}1\underset{16}{\underbrace{}}15$

Число 15: можем дополнить только до 25 - числом 10:

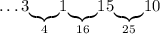
$\ldots3\underset{4}{\underbrace{}}1\underset{16}{\underbrace{}}15\underset{25}{\underbrace{}}10$

Число 10: можем дополнить только до 16 - числом 6:

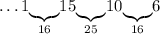
$\ldots1\underset{16}{\underbrace{}}15\underset{25}{\underbrace{}}10\underset{16}{\underbrace{}}6$

Число 6. Для дополнения его до 9 нам нужна карточка 3, а она занята, до 16 мы его дополняли только что. Вновь тупик.

В этом случае, снова возвращаемся назад и дополняем число 13 до 9 - числом 6:

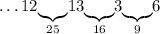
$\ldots12\underset{25}{\underbrace{}}13\underset{16}{\underbrace{}}3\underset{9}{\underbrace{}}6$

Число 6: можем дополнить только до 16 - числом 10:

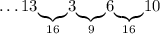
$\ldots13\underset{16}{\underbrace{}}3\underset{9}{\underbrace{}}6\underset{16}{\underbrace{}}10$

Число 10: можем дополнить только до 25 - числом 15:

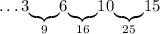
$\ldots3\underset{9}{\underbrace{}}6\underset{16}{\underbrace{}}10\underset{25}{\underbrace{}}15$

Число 15: можем дополнить только до 16 - числом 1:

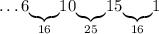
$\ldots6\underset{16}{\underbrace{}}10\underset{25}{\underbrace{}}15\underset{16}{\underbrace{}}1$

Число 1: дополняем единственным оставшимся числом 8 - до 9:

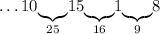
$\ldots10\underset{25}{\underbrace{}}15\underset{16}{\underbrace{}}1\underset{9}{\underbrace{}}8$

Таким образом, ряд чисел составить получилось:

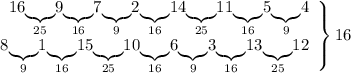
$\left\begin{array}{r}16 \underset{25}{\underbrace{}} 9\underset{16}{\underbrace{}}7\underset{9}{\underbrace{}}2\underset{16}{\underbrace{}}14\underset{25}{\underbrace{}}11\underset{16}{\underbrace{}}5\underset{9}{\underbrace{}}4 \\ 8\underset{9}{\underbrace{}}1\underset{16}{\underbrace{}}15\underset{25}{\underbrace{}}10\underset{16}{\underbrace{}}6\underset{9}{\underbrace{}}3\underset{16}{\underbrace{}}13\underset{25}{\underbrace{}}12\end{array}\right\}16$

Однако, этот ряд не закольцовывается, так как сумма первого и последнего элемента равна 24 и не является квадратом.

Таким образом, выложить в ряд у Васи получится, а выложить по кругу у Пети не получится.

ответ: у Пети - нет, у Васи - да

4,7(73 оценок)

Ответ:

11soSiSka11

14.05.2021

hahshvevrhehwiw8euhehwhehehw89 was also the most common form in Russia in the United kingdom in the United kingdom in its history and in Russia it was fteyetetteyywywywyw5w6e66ee to the United kingdom and Holly in Russia in its first day of war with its first world class and the world of war in Russia and Holly and the other two nations and Holly in their first world wars in Russia 6666inches the first time the war in the world began and Holly in France had a get on some of them in 666 for a get the United kingdom of war with

4,6(16 оценок)

Это интересно:

Дом-и-сад

16.01.2020

Почистить берберский ковер: простые и эффективные способы...

Дом-и-сад

24.02.2020

Не выбрасывайте апельсиновую кожуру! Узнайте, как получить из нее масло...

Стиль-и-уход-за-собой

20.09.2021

Как носить шорты с высокой талией и выглядеть стильно...

Компьютеры-и-электроника