ответ: 2
![arcsin \alpha \in [-\dfrac{\pi}{2};\dfrac{\pi}{2}],arccos\alpha \in [0;\pi] \:\:\forall \alpha \in R=arcsin(y-x)+arccos(x+y)\leq \dfrac{3\pi}{2}=2\pi-arcsin(y-x)-arccos(x+y)\geq 2\pi-\dfrac{3\pi}{2}0](/tpl/images/1037/3691/e7492.png)
То есть неравенство верно для всех действительных значениях переменных, удовлетворяющих области определения. Найдем ее:
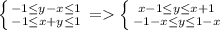
Построив 2 области и найдя их пересечение, получим область, расположенную на прикрепленном изображении на пересечении черной и красной областей (1ое и 2ое соот-но неравенства системы).
Как видим получился квадрат (1. все углы равны 90, т.к. границы задают две пары параллельных прямых, причем коэффициенты при x в парах уравнений этих прямых равны 1 и -1; 2. Все стороны равны в силу симметрии фигуры относительно осей координат) со стороной 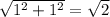
Тогда площадь равна 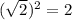
![Фигура f задаётся на координатной плоскости неравенством [tex]2\pi -arcsin(y-x)-arccos(x+y)\geq 0[/t](/tpl/images/1037/3691/eea82.jpg)
Пошаговое объяснение:
1) Будем решать с z, и никаких иксов))
2) Представь, что сыну z лет, а раз отец старше своего сыночка
не много, не мало, а в 6 раз, то и выходит, что сколько лет отцу?
Правильно мыслишь - отцу 6z лет.
3) А вот для деда - сын, это внук, ну который папин сын, понимаешь?
То-то и оно, стало быть.
4) Внуку - z лет, отцу - 6z лет, а дедок старше их обоих вместе взятых на 27 лет, вот и выходит:
z+6z+ ( z+6z+27)=83 сечёшь?)) То есть внук+отец+дед= 83.
Поехали дальше:
В этом уравнении скобки можно спокойно опустить, а потому
14z+27=83
z=(83-27)/14=56/14=4 то есть сыну 4 года.
А деду тогда 4+24+27=55 лет.