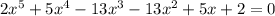
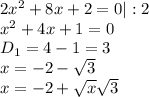

5^(x + 1) ≤ 3^(2x - 3)
логарифмируем по любому основанию или 5 или 3 (пусть 3)
log(3) 5^(x + 1) ≤ log(3) 3^(2x - 3)
(x + 1)log(3) 5 ≤ 2x - 3
2x - xlog(3) 5 ≥ 2 + log(3) 5
x (2 - log(3) 5 ) ≥ 2 + log(3) 5
2 - log(3) 5 > 0 поэтому при делении знак не меняется
x ≥ (2 + log(3) 5)/(2 - log(3) 5)
7^(x - 2) ≥ 2^(3x + 1)
логарифмируем по основанию 7
loq(7) 7^(x - 2) ≥ log(7) 2^(3x + 1)
x - 2 ≥ (3x + 1) log(7) 2
x - 3x*log(7) 2 ≥ log(7) 2 + 2
x(1 - 3log(7) 2) ≥ log(7) 2 + 2
1 - 3log(7) 2 > 0 при делении знак не меняется
х ≥ ( log(7) 2 + 2) / (1 - 3*log(7) 2)
Имеем право логарифмировать так как в обоих частях неравенства присутствую только положительные числа
Как то так Кракозябер (+)
Делим исходный многочлен на x+1 столбиком , по схеме Горнера или просто в уме.
Получаем
2x^4+3x^3-16x^2+3x+2=0
Возвратное уравнение четвёртой степени.
Замена t=x+1/x
2t^2+3t-16-2*2=0
2t^2+3t-20=0
Теорема Виетта
Сумма корней -1.5 произведение -10. Корни t= -4 и 2.5
x+1/x=-4 x+1/x=2.5
x= -2 +-√3 x=2 x=1/2
ответ : -1 ; 2 ; 1/2 ; -2+√3; -2-√3