Назови частное и остаток делимое 75; 725; 727; делитель 9; 9; 9 частное и остаток неизвесно составлено таблицей

👇

Увидеть ответ

Ответ:

Sarzhanovaperuza

03.02.2021

75:9=8(ост.3)
725:9=80(ост.5)
727:9=80(ост.7)

4,8(21 оценок)

Открыть все ответы

Ответ:

kattun

03.02.2021

Найдём все n, для которых пример вообще может существовать. Для этого сложим все a_i_j, которые у нас есть (i - номер многочлена, j - номер места). С одной стороны, должно получиться 26n, так как такова сумма для изначального многочлена. С другой стороны, для каждого многочлена из суммы сумма коэффициентов равна n*(n+1)/2. Тогда 26n ⋮ n(n+1)/2 => 26 ⋮ (n+1)/2 => 52 ⋮ n+1 => n = {1, 3, 12, 25, 51}. Теперь давайте подумаем и поймём, что n = 1 и n = 3 не подходят, так как в таком случае различных многочленов будет 1 и 6 соответственно, а нужно не менее 26 и 13 различных многочленов соответственно, а n = 51 не подходит, так как тогда одно из слагаемых будет равно 51, что больше 26.

Приведём пример для n = 25: a_1_1 = 1, a_1_2 = 2, ... , a_1_25 = 25, a_2_i = a_1_(26-i). Тогда a_1_i + a_2_i = 26. Аналогично для n = 12, только нужно будет 4 многочлена, из которых одна пара строится таким же образом, а другая пара - с переменой мест, например, 1 и 2. Тогда все многочлены различны.

ответ: n = 12 или n = 25.

4,5(78 оценок)

Ответ:

ДашаСалина

03.02.2021

Пошаговое объяснение:

$\left[\begin{array}{ccc}3&2&1\\0&1&2\\\end{array}\right] *\left[\begin{array}{ccc}1\\2\\3\end{array}\right]=c$

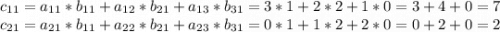
$c_{11} = a_{11} *b_{11} + a_{12}*b_{21} + a_{13}*b_{31} = 3*1 + 2*2 + 1 *0 = 3 + 4 + 0 = 7\\c_{21} = a_{21}* b_{11} + a_{22}* b_{21} + a_{23} *b_{31} = 0*1 + 1*2 + 2*0 = 0 + 2 + 0 = 2$

$c=\left[\begin{array}{ccc}7\\2\\\end{array}\right]$

$\left[\begin{array}{ccc}3&5\\6&1\\\end{array}\right] *\left[\begin{array}{ccc}2&1\\-3&2\\\end{array}\right] =c$

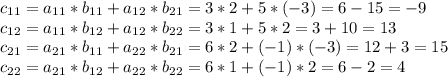
$c_{11} = a_{11}*b_{11} + a_{12}*b_{21} = 3* 2 + 5 *(-3) = 6 - 15 = -9\\c_{12} = a_{11}*b_{12} + a_{12}*b_{22} = 3 *1 + 5*2 = 3 + 10 = 13\\c_{21} = a_{21}*b_{11} + a_{22}*b_{21} = 6*2 + (-1)*(-3) = 12 + 3 = 15\\c_{22} = a_{21}*b_{12} + a_{22} * b_{22} = 6*1 + (-1)*2 = 6 - 2 = 4$

$c= \left[\begin{array}{ccc}-9&13\\15&4\\\end{array}\right]$

$A=\left[\begin{array}{ccc}-3&2\\5&-4\\\end{array}\right]$

для вычисления обратной матрицы запишем матрицу А, дописав к ней справа единичную матрицу:

$\left[\begin{array}{cccc}-3&2&1&0\\5&-4&0 &1\\\end{array}\right]$

теперь чтобы найти обратную матрицу, преобразуем левую часть полученной матрицы в единичную.

1-ую строку делим на -3

$\left[\begin{array}{cccc}1&-2/3&-1/3&0\\-5&4&0&1\\\end{array}\right]$

1 строку * 5 к 2ой добавляем 1 строку

$\left[\begin{array}{cccc}-1&-2/3&-1/3&0\\0&-7\frac{1}{3} &-1\frac{2}{3} &1\\\end{array}\right]$

2-ую строку делим на 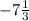$-7\frac{1}{3}$

$\left[\begin{array}{cccc}1&-2/3&-1/3&0\\0&1&5/22&-3/22\\\end{array}\right]$

и последнее 2ую * (2/3) и к 1 строке добавляем 2ую

$\left[\begin{array}{cccc}1&0&-2/11&-1/11\\0&1&5/22&-3/22\\\end{array}\right]$

и вот

$A^{-1}=\left[\begin{array}{ccc}-2/11&-1/11\\5/22&-3/22\\\end{array}\right]$

определитель матрицы А:

∆A = 1*1 - 2*1 = -1

nак как A невырожденная матрица, то существует обратная матрица A⁻¹

Умножим справа обе части уравнения на A⁻¹: X·A·A⁻¹ = B·A-1, откуда находим, что X = B·A⁻¹

найдем обратную матрицу A⁻¹.

транспонированная матрица

$A^T=\left[\begin{array}{ccc}1&2\\1&1\\\end{array}\right]$

aлгебраические дополнения

A₁₁ = (-1)¹⁺¹ *1 = 1; A₁₂ = (-1)¹⁺² *1 = -1;

A₂₁ = (-1)²⁺¹ *2 = -2; A₂₂ = (-1)²⁺² *1 = 1;

обратная матрица

$A^{-1}=\left[\begin{array}{ccc}1&-1\\-2&1\\\end{array}\right]$

тогда

$X=\left[\begin{array}{ccc}3&2\\-1&3&\\\end{array}\right] *\frac{1}{-1} \left[\begin{array}{ccc}1&-1\\-2&1\\\end{array}\right] =\left[\begin{array}{ccc}1&1\\7&-4\\\end{array}\right]$