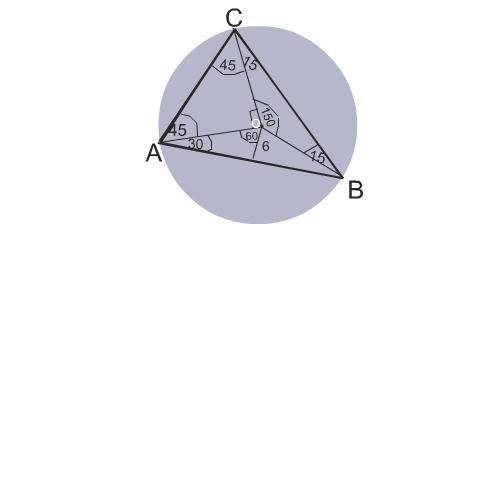
Радиусами окружности исходный треугольник АВС делится на 3 равнобедренных треугольника.
В трегольнике СОВ острые углы равны по 15 градусов, поэтому
угол СОВ равен 180-30=150 градусов.
Угол СОА равен 90 градусов по условию задачи.
Отсюда
угол АОВ равен 360 -90-150=120 градусов.
Расстояние от О до АВ равно 6 см.
Этот отрезок делит треугольник АОВ на два прямоугольных треугольника,острый угол ОАВ равен 30 градусов.
Радиус ОА в этом треугольнике является гипотенузой и вдвое больше катета, противолежащего углу 30 градусов.
Радиус окружности равен
6*2=12 см
Пошаговое объяснение:
(x-3)(2x+5)<(2x-6)(2x-1)
2x²+5x-6x-15<4x²-2x-12x+6
2x²-x-15<4x²-14x+6
4x²-14x+6-2x²+x+15>0
2x²-13x+21>0
Допустим:
2x²-13x+21=0; D=169-168=1
x₁=(13-1)4=12/4=3
x₂=(13+1)/4=14/4=7/2=3,5
Нанесём точки на ось x. Выбираем точку из любого интервала для проверки знака на интервале, например 0:
2·0²-13·0+21>0; 21>0⇒знак на интервале, в котором лежит точка 0 будет +.
+ - +
..> x
3 3,5
(-∞<x₁<3)∨(3,5<x₂<+∞)
ответ: x∈(-∞; 3)∪(3,5; +∞).
L=3,14*6=18,84 см