Изменение баланса Упражнение 1.
На 01.01.0х известны следующие данные по фирме:
1. Имущество 500 тыс. крон
2. Обязательства 100 тыс. крон
3. Собственный капитал 400 тыс. крон
Операции за месяц:
• Собственники внесли денежный взнос в счет пополнения акционерного капитала 200 тыс. крон
• Купили оборудование в кредит за 500 тыс. крон
Объем баланса фирмы на конец месяца составит тыс.крон.
Упражнение 2.
02.01.0х получен счет поставщика за аренду за январь. Какие изменения произойдут:
№ Имущество Обязательство Собственный капитал Доходы Расходы прибыль
1 увеличение уменьшение не изменится уменьшение увеличение уменьшение
2 уменьшение увеличение увеличение уменьшение не изменится уменьшение
3 не изменится увеличение уменьшение не изменится увеличение уменьшение
4 не изменится увеличение уменьшение уменьшение увеличение уменьшение
Какой вариант будет верным?
Верный вариант под номером
Упражнение 3.
На начало 200х года имущество фирмы составило 500 тыс. крон, обязательства 200 тыс. крон, собственный капитал 300 тыс. крон.
Операции за отчетный период:
• Фирма купила в кредит оборудование на сумму 100 тыс. крон,
• Денежный взнос в паевой капитал 160 тыс.крон
В результате данных операций в балансе на 31.12. 0х года:
1. Имущество тыс.крон
2. Обязательства тыс.крон
3. Собственный капитал тыс.крон
очевидно при n = 1 не существует графа с 2 ребрами, поэтому n ≥ 2
степень вершины - количество всех ребер, выходящих из вершины deg(v)
сумма степеней всех вершин равна удвоенному количеству всех ребер
т.е. в данном графе сумма степеней вершин
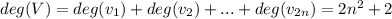
будем доказывать от противного. предположим такого ребра нет.
рассмотрим любые 4 вершины, чтобы среди них не было ребра, которое принадлежит двум циклам длины 3, среди них может быть проведено не более 4 ребер, как бы не проводили пятое, всегда оно дополнит второй цикл.
поэтому сумма степеней всех вершин среди любых четырех не превосходит 4*2 = 8
рассмотрим четверки:
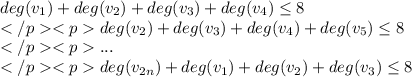
сложим все неравенства и получим, что
4*deg(V) ≤ 16n
deg(V) ≤ 4n
но deg(V) по условию равно 2n² + 2
2n² + 2 ≤ 4n
2(n-1)² ≤ 0
неравенство может выполниться только при n = 1, но как уже было отмечено, этот случай не удовлетворяет по условию.
Значит, наше предположение было не верно.
ответ: доказано.
(24*30)+(24*5)-720+120-840
2)840:35-840:(7*5)(опять разкладываем чтобы было легче)-24
3)80*32-80*(30+2)(опять раскладываем)-(80*2)+(80*30)-160+2400-2560
и 4)2560:32-2560:(8*4)-80
надеюсь вам понятно