Произведение чисел 13/54 и 18/65 произведение чисел 28/65 и 13/35 в классе 28 учащихся, девочки составляют 5/7 числа всех учащихся класса. сколько девочек в классе? у коровы 32 зуба, что составляет 8/11 числа зубов свиньи. сколько зубов у свиньи? ответ запишите числом без наименования. у мыши 16 зубов, что составляет 4/7 числа зубов кролика. сколько зубов у кролика? ответ запишите числом без наименования.

👇

Ответ:

likaizmaylova

28.09.2022

13/54*18/65=13/65*18/54=1/5*1/3=1/15
28/65*13/35=13/65*28/35=1/5*4/5=4/25
Девочек 5/7*28=5*28/7=5*4=20
Зубов у свиньи 32*11/8=11*32/8=11*4=44
Зубов у кролика 16*7/4=7*16/4=7*4=28

4,8(81 оценок)

Открыть все ответы

Ответ:

adelya63Ada

28.09.2022

Решим сначала однотипное однородное ДУ

y''+2y'+y=0

Составляем характеристическое уравнение:

k²+2k+1=0

$k _{1,2} = - 1$

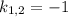
Общее решение ОДУ:

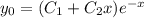
$y_0=(C_1+C_2x)e^{-x}$

Заметим, что "кратный корень" правой части исходного уравнения: k=0, так как справа стоит -2х (то есть многочлен)

Но при решении характеристического уравнения получились другие корни (k=-1), поэтому на частное решение это никак не повлияет.

Частное решение ДУ— это общий вид правой части:

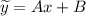
$\widetilde{y} = Ax+B$

Найдем 1 и 2-ю производные

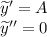
$\widetilde{y}' = A \\ \widetilde{y}''= 0$

Подставляем частное решение в исходное ДУ:

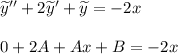
$\widetilde{y}'' + 2 \widetilde{y}' + \widetilde{y} = - 2x \\ \\ 0 + 2A + Ax+B = - 2x$

Теперь приравниваем слагаемые:

Слева перед икс стоит А, справа перед икс стоит -2, значит

А=-2

Слева свободные члены: 2А+В, справа нет свободных членов, значит 0

2A+B=0

2*(-2)+B=0

-4+B=0

B=4

Тогда

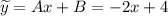
$\widetilde{y} = Ax+B = - 2x + 4$

Решие данного ДУ:

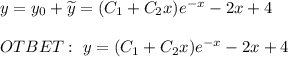
$y = y _{0} + \widetilde{y} = (C_1+C_2x)e^{-x} - 2x + 4 \\ \\ OTBET: \ y = (C_1+C_2x)e^{-x} - 2x + 4$

4,4(18 оценок)

Ответ:

musaevakhadizh

28.09.2022

Мои родители купили мне собаку, кошку, попугая и рыбу. Я решил исследовать их движения.Итак. Если мы будем наблюдать, то сразу заметим, что исключая движение кошки и собаки, все они двигаются по-разному. Если посмотрим ещё внимательней и подумаем, то вспомними, что и собака, и кошка, и попугай имеют гомологичные органы, которые сформировались в процессе дивергенции. А если более внимательно - то заметим, что все эти животные, абсолютно все! используют для движения свои органы: кошки и собаки - лапы (пятипалую конечность), попугай - крылья (пятипалая конечность), а рыба - плавники. Т.е! Для того, чтобы двигаться, им необходимы специальные двигалки - лапки, крылья, плавники, без которых было бы невозможно движение.Вывод: без особых при пятипалые конечности и плавники), необходимых для передвижения, купленные моими родителями животные, не смогли бы передвигаться.

4,6(87 оценок)

Это интересно:

Здоровье

08.08.2020

8 советов по подготовке к приему к стоматологу: как не бояться и что вам нужно знать...

Финансы-и-бизнес

21.12.2022

Как выбрать и купить восстановленный деревянный стол...

Компьютеры-и-электроника

18.01.2021

Как правильно пинговать IP адрес: простой гайд для начинающих...

Образование-и-коммуникации