Pabs = 48 cм a: b: c=3: 4: 5 найдите abc

Question

Математика: Pabs = 48 cм a: b: c=3: 4: 5 найдите abc

катя19052 · Accepted Answer

Пошаговое объяснение:

Составим каноническое уравнение прямой

Воспользуемся формулой канонического уравнения прямой:

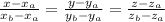
$\frac{x-x_{a} }{x_{b} -x_{a} } =\frac{y-y_{a} }{y_{b} -y_{a} }=\frac{z-z_{a} }{z_{b} -z_{a} }$

Подставим в формулу координаты точек:

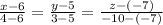
$\frac{x - 6}{4 - 6} =\frac{y - 5}{3 - 5} =\frac{z - (-7)}{-10 - (-7)}$

В итоге получено каноническое уравнение прямой:

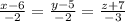
$\frac{x - 6}{-2} =\frac{y - 5}{-2} =\frac{z +7}{-3}$

Составим параметрическое уравнение прямой

Воспользуемся формулой параметрического уравнения прямой:

x = l t + x₁

y = m t + y₁

z = n t + z₁ где {l; m; n} - направляющий вектор прямой, в качестве которого можно взять вектор AB;

(x₁, y₁, z₁) - координаты точки лежащей на прямой, в качестве которых можно взять координаты точки A.

координаты вектора AB = {4 - 6; 3 - 5; -10 - (-7)} = {-2; -2; -3}

В итоге получено параметрическое уравнение прямой:

x = - 2t + 6

y = - 2t + 5

z = - 3t - 7