Максимальное количество оказывается в ряде 2,...,11. Это 2,3,5,7,11, то есть 5.
В ряде 3,...,12 это 3,5,7,11, то есть 4.
В ряде 6,...,15 это 7,11,13, то есть 3.
В ряде 20,...,29 это 23,29, то есть 2.
В ряде 90,...,99 это 97, то есть 1.
В ряде 200,..,209 простых чисел нет, то есть 0.
ответ: в ряде из 10 последовательных натуральных чисел может быть от 0 до 5 (включительно) простых чисел.
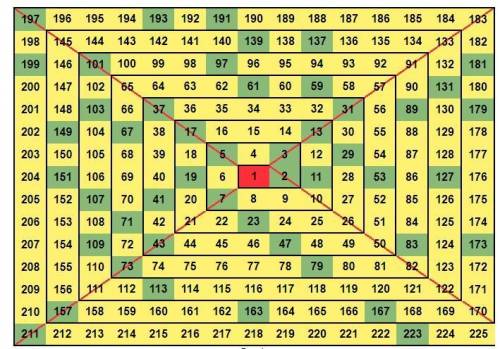
Картинка с числами до 225 приложена. В ней зеленым отмечены простые числа. (1, кстати, не является простым числом, она красным отмечена)
2x³-2x²+x²-1=0
(x-1)*(2x²+x+1)=0
x-1=0 2x²+x+1=0
x=1 D=(1)²-4*2*1=-6
D≠-6 t.k. D<0
Otvet: x=1
3) x⁴+x³+x²-x-2=0
(x-1)*(x³+2x²+3x+2)=0
(x-1)*(x+1)*(x²+x+2)=0
x-1=0 x+1=0 x²+x+2=0
x₁=1 x₂=-1 D=(1)²-4*1*2=-5
D≠5 t.k. D<0
Otvet: x₁=1 ; x₂=-1