Пошаговое объяснение:
Составим каноническое уравнение прямой
Воспользуемся формулой канонического уравнения прямой:
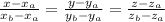
Подставим в формулу координаты точек:
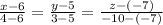
В итоге получено каноническое уравнение прямой:
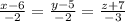
Составим параметрическое уравнение прямой
Воспользуемся формулой параметрического уравнения прямой:
x = l t + x₁
y = m t + y₁
z = n t + z₁ где {l; m; n} - направляющий вектор прямой, в качестве которого можно взять вектор AB;
(x₁, y₁, z₁) - координаты точки лежащей на прямой, в качестве которых можно взять координаты точки A.
координаты вектора AB = {4 - 6; 3 - 5; -10 - (-7)} = {-2; -2; -3}
В итоге получено параметрическое уравнение прямой:
x = - 2t + 6
y = - 2t + 5
z = - 3t - 7
Рассчитаем скорость сгорания каждой свечи.
24:6=4 см/час скорость сгорания первой свечи
24:4=6 см/ч скорость сгорания второй свечи.
Пусть третья свеча сгорела за х часов. Тогда за это же время сгорело 4х см первой свечи, и 6х см второй свечи. По условию огарок от первой свечи в 2 раза длиннее огарка второй свечи. Найдем длины огарков:
(24-4х) см остаток первой свечи, (24-6х) см остаток второй свечи.
Составим уравнение:
24-4х=2(24-6х)
24-4х=48-12х
12х-4х=48-24
8х=24
х=3 часа время за которое сгорела третья свеча.
ответ 3 часа
=
[ (5^2• 2^2- 2^3 •3• 2^2- 7^2• 2^2)^2]^6=
[ {2^2 • (5^2- 2^3• 3- 7^2) }^2 ]^6=
[{ 2^2• (5•5- 2•2•2•3- 7•7)}^2]^6=
[{2^2•(25-24-49)}^2 ]^6=
[{2^2• (-50)}^2]^6=
[{2^2• (-(5•5•2)}^2]^6=
Степень четная (-) исчезнет
[ (2•2• 5•5•2)^2]*6=
[(10•10•2)^2]^6=
[(10^2• 2)^2]^6=
[10^4• 2^2]^6=
10^24• 2^12 =
(10^2)^12• 2^12=
(100•2)^12=
200^12=
200.000.000.000.000