Что мы будем использовать: последовательность 
монотонно возрастает и имеет конечный предел; этот предел обозначается буквой e. Первые цифры числа e все знают. Для нас достаточно знать, что
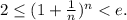
1) 
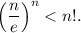При n=1 неравенство очевидно. Предположим, что оно справедливо при некотором n, и докажем, что тогда оно справедливо при n+1. Итак, нужно доказать, что 
Имеем:
2) 
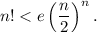При n=1 неравенство очевидно. Предположив, что при некотором n неравенство справедливо, докажем, что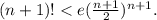 
Имеем:
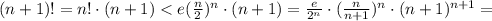
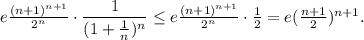
Доказательство завершено благодаря тому, что все натуральные числа расположены "по порядку" одно за другим, и есть первое натуральное число (принцип домино: если доминошки расположить на боку одну рядом с другой на небольшом расстоянии друг от друга в виде змеи, и уронить первую доминошку на вторую, то вторая упадет на третью, третья на четвертую и так далее, пока не упадут все).
это решение системы
х²-5х+6>0; х²-5х+6=0; по теореме, обратной теореме ВИЕТА, находим корни уравнения х=2;х=3, значит, х²-5х+6=(х-2)(х-3), тогда
(х-2)(х-3)>0
(2-x)/(x-3)≥0⇒(x-2)/(x-3)≤0
второе неравенство равносильно системе
(x-2)(x-3)≤0;
х≠3
Т.о., для решения вопроса области определения данной функции надо решить такую систему
(х-2)(х-3)>0
(x-2)(x-3)≤0;
х≠3
как видим, одновременно произведение (х-2)(х-3) и быть большим или равным нулю и быть меньшим нуля при х≠3, быть не может. поэтому данная функция не определена ни при каких значениях х.
Зимний лес похож на заколдованное царство Снежной королевы. Здесь стоит тишина. Пушистый белоснежный покров устилает землю. Он также наброшен на ветви деревьев, как шубы.
Кажется, будто деревья в зимнем лесу одели сказочные наряды. Все вокруг украшено слепящим снегом, прозрачным льдом и серебристым инеем. Лес полон хрупких зимних драгоценностей.
Только ветви замерзших деревьев иногда скрипят и трещат от мороза. Да похрустывание снега под ногами нарушает тишину во время прогулки по зимнему лесу. Но вообще-то зимой здесь трудно пройти. Можно провалиться в сугроб по колено, а то и по пояс.
Когда идешь зимним лесом, кажется, что в лесу нет ни единой живой души. Как будто все птицы, звери и насекомые покинули эти края в поисках тепла или залегли в спячку. Даже вороны подались в город, кормиться около людей. Но в этот же момент заяц-беляк, невидимый на снегу, наблюдает за путешественниками. Жизнь в зимнем лесу затихает, но не останавливается.