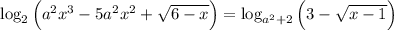
Раз некоторое число  удовлетворяет уравнению при любом
удовлетворяет уравнению при любом  , то оно также удовлетворяет уравнению при
, то оно также удовлетворяет уравнению при 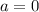 .
.
То есть, если мы подставим в уравнение 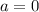 , то выполнится равенство:
, то выполнится равенство:
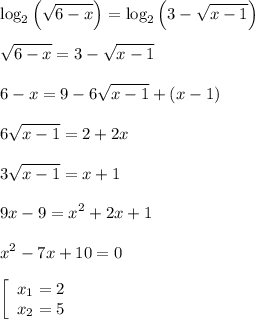
Оба корня удовлетворяют уравнению и ОДЗ (при 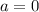 ): с обеих сторон в первом случае получается
): с обеих сторон в первом случае получается  , а во втором
, а во втором 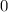 (так как мы не выписывали ОДЗ, то мы могли получить "лишние корни", но мы их не получили).
(так как мы не выписывали ОДЗ, то мы могли получить "лишние корни", но мы их не получили).
Очевидно, что эти два корня в ответ так сразу не пойдут. Мы знаем лишь только, что они подходят при 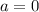 . И если ответ на задачу существует, то он может быть только
. И если ответ на задачу существует, то он может быть только 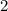 ,
, 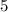 или и
или и 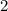 , и
, и 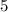 . Но про другие значения
. Но про другие значения  мы пока ничего не знаем.
мы пока ничего не знаем.
Посмотрим, что у нас будет получаться при 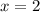 :
:
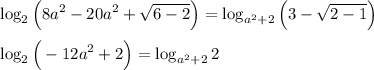
Вот только первый логарифм не всегда существует. 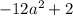 может быть отрицательным (возьмите, к примеру,
может быть отрицательным (возьмите, к примеру, 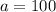 ). А подлогарифмическое выражение обязано быть положительным. Значит, такой
). А подлогарифмическое выражение обязано быть положительным. Значит, такой  нас не устраивает.
нас не устраивает.
Теперь проверим 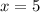 :
:
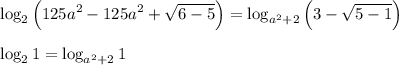
В обеих частях мы получили 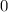 (так как
(так как 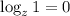 , если
, если 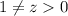 ). Также
). Также 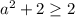 , поэтому все ограничения будут выполняться.
, поэтому все ограничения будут выполняться.
В итоге имеем нужный ответ: 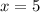 .
.
Задача решена!
Это показательное уравнение вида 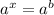 , где
, где 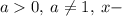 неизвестная переменная.
неизвестная переменная.
Если сделаем основания степени равными, то по правилу сможем приравнять показатели степеней и решить обычное линейное уравнение.
Для этого, нужно член уравнения 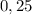 представить в виде числа со степенью так, чтобы в основании было число
представить в виде числа со степенью так, чтобы в основании было число 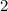 . Это явно число
. Это явно число 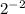 (проверка:
(проверка: 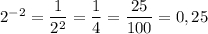 ).
).
Значит теперь, когда наше показательное уравнение имеет вид 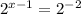 , то можем приравнять показатели степени и получим стандартное линейное уравнение. Решение этого уравнения и будет являться корнем исходного показательного уравнения.
, то можем приравнять показатели степени и получим стандартное линейное уравнение. Решение этого уравнения и будет являться корнем исходного показательного уравнения.
Итак, мы получили уравнение 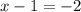 после того, как приравняли показатели степени. Решаем это уравнение. Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое. Т.е.
после того, как приравняли показатели степени. Решаем это уравнение. Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое. Т.е. 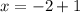 .
.
Из этого следует, что ответ нашего показательного уравнения равен 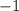 .
.

S = 20 км; t = 40 мин = 40/60 ч = 2/3 ч - двигался по шоссе
S = 600 м = 600/1000 км = 3/5 км ; t = 2 мин = 2/60 ч = 1/30 ч - двигался по тропинке
S = 20 + 3/5 = 20 целых 3/5 = 103/5 (км) - весь путь;
t = 2/3 + 1/30 = 20/30 + 1/30 = 21/30 (ч) - время в пути;
v =103/5 : 21/30 = 103/5 * 30/21 = (103*6)/(1*21) = 618/21 = 29 целых 9/21 = 29 целых 3/7 (км/ч) - средняя скорость движения.
Вiдповiдь: 29 цiл. 3/7 км/год.