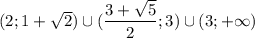
Пошаговое объяснение:
ОДЗ логарифмов: x > 0, x ≠ 1, x > 2, x ≠ 3 ⇒ x > 2, x ≠ 3
Пусть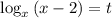 
. Тогда 
:
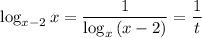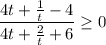. Заметим, что t ≠ 0, так как это значение достигается только при x = 3 (x - 2 = x⁰ = 1 ⇔ x = 3). Но при x = 3 основание логарифма 
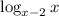равно 1, что не удовлетворяет ОДЗ. Значит, домножим обе части дроби на t:
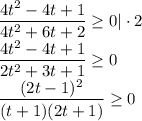
Решим методом интервалов:
+ - + +
----o----o----*---->
-1 -¹/₂ ¹/₂
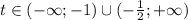
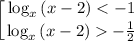
Заметим, что по ОДЗ x > 2, то есть основание логарифма всегда больше 1. Значит, на ОДЗ неравенства равносильны:
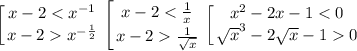
Первое неравенство имеет решение (с учётом ОДЗ)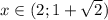 
Второе неравенство раскладывается на множители:
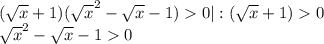
Нули получившегося неравенства: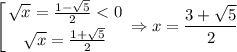 
C учётом ОДЗ получаем, что в данном случае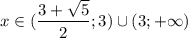 
(левая граница меньше правой, так как √5 < 3).
Объединим промежутки. Сравним правую границу первого неравенства и левую границу второго. Сравним эти числа относительно 2,5:
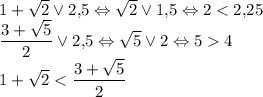
Тогда промежутки не пересекаются, итоговый ответ: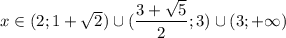 
Относится это растение к высоким кустарниковым либо к невысоким (до 10 метров) деревьям. Словно красавица-невеста, она надевает белое одеяние во время цветения (май-июнь) и превращается в какое-то чудо. В июле — августе появляются плоды, ягодки диаметром от 8-ми до 10-ти миллиметров, по мере созревания превращаются из зелёного в красный, и в конце - в чёрный цвет. В народе бытует такое мнение - расцвела черёмуха - жди холодов. Это обусловлено тем, что погодные периоды совпадают со временем цветения черёмухи.
9-8=1
1+8=9
8+1=9
9-1>9-8