S, км V, км/ч t, ч
Л. 2x x 2
Г. 5(x-48) x-48 5
Пусть x км/ч - скорость легковой машины, тогда (x-48) км/ч - скорость грузовика. Составляем уравнение:
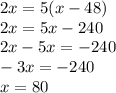
80 км/ч - скорость движения легковой машины.
2) 80 - 48 = 32 км/ч - скорость движения грузовика.
ответ: 80 км/ч; 32 км/ч
ответ: 15
Пошаговое объяснение:1.Найдётся 12 рогаликов на которых есть глазурь и сахарная пудра – неверно, так как глазурью покрыто только 10!
2.Найдётся 5 рогаликов на которых нет ни глазури ни сахарной пудры
Верно. 10 в глазури, 20 в сахарной пудре, всего 35.
Если глазированные и покрытые сахарной пудрой не пересекаются. то все равно есть 5 не покрытых ни глазурью, ни сахарной пудрой.
3.Рогаликов на которых есть и глазурь и сахарная пудра не может оказаться меньше 14
Нет. Так как покрытых глазурью 10.
4.рогаликов на которой нет ни глазури и нет ни сахарной пудры не может оказаться больше 15
Нет. Если все рогалики, которые покрыты глазурью, посыпать сахарной пудрой, то останется 10 рогаликов, которые покрыты только сахарной пудрой
10+10=20
35–20=15
Может быть, что останется ровно 15, но больше 15–ти непокрытых никогда не останется.
x^2 - 10b*x + (81b^2 + 2b - 12) = 0
D/4 = (-5b)^2 - (81b^2 + 2b - 12) = 25b^2 - 81b^2 - 2b + 12 = -56b^2 - 2b + 12
Два корня есть, когда D/4 > 0
-56b^2 - 2b + 12 > 0
56b^2 + 2b - 12 < 0
D = 2^2 - 4*56(-12) = 4 + 2688 = 2692 = (2√673)^2
b1 = (-2 - 2√673)/112 = (-1 - √673)/56 ≈ -0,48; b2 = (-1 + √673)/56 ≈ 0,44
b ∈ ((-1 - √673)/56; (-1 + √673)/56) - при этих b у уравнения 2 корня.
Но нам надо, чтобы один корень был меньше 2, а другой больше 2.
{ x1 = 5b - √(-56b^2 - 2b + 12) < 2
{ x2 = 5b + √(-56b^2 - 2b + 12) > 2
Корень арифметический, то есть неотрицательный.
Оставляем корни отдельно
{ 5b - 2 < √(-56b^2 - 2b + 12)
{ √(-56b^2 - 2b + 12) > 2 - 5b
1) Если b <= 2/5 = 0,4, то первое неравенство верно при любых b ∈ ОДЗ.
Потому что будет 5b - 2 <= 0. Значит, b ∈ ((-1 - √673)/56; 0,4]
Второе неравенство возводим в квадрат
-56b^2 - 2b + 12 > 4 - 20b + 25b^2
81b^2 - 18b - 8 < 0
D/4 = 9^2 - 81*(-8) = 81 + 648 = 729 = 27^2
b1 = (9 - 27)/81 = -18/81 = -2/9 ≈ -0,222 > (-1 - √673)/56 ≈ -0,48
b2 = (9 + 27)/81 = 36/81 = 4/9 ≈ 0,444 < (-1 + √673)/56 ≈ 0,445
Но b <= 0,4, поэтому
b ∈ (-2/9; 0,4] - ЭТО РЕШЕНИЕ.
2) Если b >= 0,4, то второе неравенство верно при любых b ∈ ОДЗ.
Потому что будет 2 - 5b < 0. Значит, b ∈ [0,4; (-1 + √673)/56)
Первое неравенство возводим в квадрат
25b^2 - 20b + 4 < -56b^2 - 2b + 12
81b^2 - 18b - 8 < 0
Неравенство получилось такое же, и решение у него такое же:
b ∈ (-2/9; 4/9)
Промежуток b ∈ [0,4; (-1 + √673)/56) входит в это решение, поэтому
b ∈ (0,4; (-1 + √673)/56) - ЭТО РЕШЕНИЕ.
ответ: Промежуток: b ∈ (-2/9; (-1 + √673)/56)
Длина этого промежутка с точностью до 3 знаков после запятой:
0,44539 + 0,22222 = 0,66761 ≈ 0,668