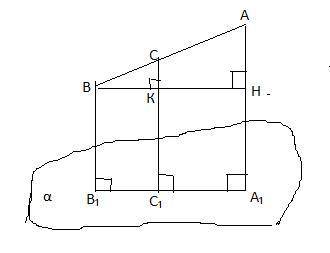
Даны плоскость α и не пересекающий данную плоскость отрезок AB. На этом отрезке взята точка C так, что AC : CB = 3 : 2. Найдите расстояние (cm) от точки C до плоскости α, если расстояния из концов отрезка AB до плоскости равны AA1=18 cm и BB1=13 cm.
Пошаговое объяснение:
Т.к. AC : CB = 3 : 2 ,то АВ составляет 5 частей, ВС-две части отрезка АВ.
Т.к. в задаче идет речь о расстояниях , то АА₁⊥α, СС₁⊥α , ВВ₁⊥α ⇒ АА₁║СС₁║ВВ₁.
Пусть ВН⊥АА₁ ⇒АН=18-13=5 (см) . Отрезок СС₁=СК+КС₁ .
ΔАВН подобен ΔСВК по 2 углам :∠В -общий,∠ВКС=∠ВНА=90° ⇒ сходственные стороны пропорциональны :
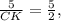 СК=2 см.
СК=2 см.
СС₁=2+13=15 (см)
Пошаговое объяснение:
Диагональ прямоугольника равна по теореме Пифагора :
sqrt ( 6^2+ 8^2) =10( см). В прямоугольном треугольнике с высотой пирамиды гипотенуза равна 13 см, один из катетов - 5см ( половина диагонали прямоугольника). Высота по теореме Пифагора равна sqrt(13^2 - 5^2)=12(см). Площадь полной поверхности складывается из площади основания, площадей двух пар равных боковых граней. Площадь основания равна 6х8=48 (кв. см). Апофемы ( высоты боковых граней ) находятся из прямоугольных треугольников с высотами пирамиды. Вторые катеты равны половине сторон основания. Т.о. одна апофема по теореме Пифагора равна sqrt (12^2 + 4^2)=4 sqrt 10. Другая апофема равна sqrt(12^2 +3^2)=sqrt 153. Площадь боковой грани с первой апофемой равна 6х4sqrt 10/2=12 sqrt 10. Площадь боковой грани со второй апофемой равна 8хsqrt 153 /2= 4 sqrt 153. И площадь полной поверхности пирамиды равна ( 48 + 24 sqrt 10+ 8 sqrt 153) кв. см.
2 задача. 2 боковые ребра находятся из прямоугольных треугольников, содержащих высоту пирамиды, а второй катет - половина известной диагонали (6:2=3). Мы получаем египетский треугольник : катеты равны 4 см и 3 см , поэтому боковое ребро = 5 см. Чтобы найти оставшиеся боковые рёбра, надо
2)303804:6=50634
3)316351+ 50634=366985
Таким нельзя? Именно в столбик нужно?