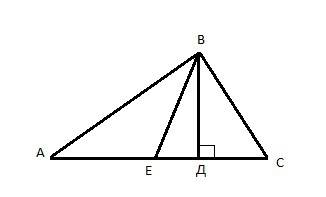
Построим треугольник АВС (Сторона АС=8 см.) Проведем к стороне АС высоту ВД (4 см) и медиану ВЕ (5 см). см. приложение.
1. Рассмотрим треугольник ВДЕ: угол ВДЕ=90 градусов. Катет ВД=4 см. Гипотенуза ВЕ=5 см
По теореме Пифагора найдем ДЕ:
ДЕ=√(ВЕ^2-ВД^2)= √(5^2-4^2)= √(25-16)= √9=3 см.
Так как ВЕ – медиана АЕ=СЕ=8/2=4 см.
Зная это найдем СД и АД:
СД=СЕ-ДЕ=4-3=1 см.
АД=АЕ+ДЕ=4+3=7 см.
2. Найдем сторону АВ.
Рассмотрим треугольник АВД – угол АДВ= 90 градусов. Катет АД=7см. Катет ВД=4 см.
По теореме Пифагора найдем АВ:
АВ=√(АД^2+ВД^2)= √(7^2+4^2)= √(49+16)= √65 см (приблизительно 8,06 см)
3. Найдем сторону ВС.
Рассмотрим треугольник ВСД – угол ВДС= 90 градусов. Катет СД=1см. Катет ВД=4 см.
По теореме Пифагора найдем АВ:
ВС=√(СД^2+ВД^2)= √(1^2+4^2)= √(1+16)= √15 см (приблизительно 3,87 см)
ответ: АВ= √65 см. ВС= √15 см
Тогда голов: 3х+у=26.
Ног всего: 40у+ах=298.
Решаем систему:
3х+у=26 (1)
40у+ах=298 (2)
Из (1) выразим у и подставим в (2):
у=26-3х
40(26-3х)+ах=298
1040-120х+ах=298
120х-ах=742
х(120-а)=2*7*53.
Подбираем:
1) х=2: 120-а=371
а=-251<0 не может быть.
2) х=7: 120-а=106;
а=14.
у=26-3*7=5.
40*5+14*7=298
298=298 (верно), а=14.
3) х=53: у=26-3*53<0 не может быть.
ответ: у каждого дракона 14 ног.