В прямоугольном параллелепипеде все грани - прямоугольники, все рёбра равны и перпендикулярны основаниям.
Формула диагонали квадрата d=a√2 ⇒
Диагональ АС основания равна 4√2
Из прямоугольного треугольника АА1С по т.Пифагора боковое ребро
АА1=√(А1С²-AC²)=√(81-32)=7 (ед. длины)
-------
Вариант решения.
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.
Измерениями прямоугольного параллелепипеда являются длины трех ребер, исходящих из одной его вершины. Отсюда следует:
D²=a²+b²+c², где а и b- стороны основания, с - боковое ребро.
По условию а=b=4. D=9
81=16+16+c² ⇒
c²=81-32=49
c=7 - длина бокового ребра.

Чтобы найти промежутки возрастание/спадания функции и её экстремумы, нужно приравнять её производную к нулю:
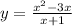
Найдём производную про правилу: 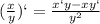 :
:
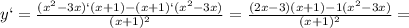
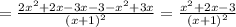
Приравняем производную к нулю:
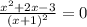
Знаменатель не может быть равен нулю, значит приравняем к нему только числитель:
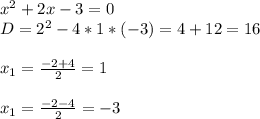
Получили экстремумы функции.
Воспользуемся методом интервалов для нахождения промежутков возрастания и спадания функции. Т.к. возле старшего коэффициента стоит плюс, начинаем с плюса:
+ - +
-------(-3)----------(1)----------->
Функция возрастает на (-∞; -3] и [1; +∞)
Функция спадает на [-3; 1]
x = -3 - точка максимума
x = 1 - точка минимума
|-1
||-2
|||-3
|V-4
V-5