ответ: min y = -3, max y = -1.
Пошаговое объяснение:
Находим производную.
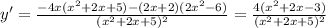
Приравниваем нулю множитель числителя с переменной.
Решаем уравнение x^2+2*x-3=0.
Ищем дискриминант:
D=2^2-4*1*(-3)=4-4*(-3)=4-(-4*3)=4-(-12)=4+12=16;
Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√16-2)/(2*1)=(4-2)/2=2/2=1;
x_2=(-√16-2)/(2*1)=(-4-2)/2=-6/2=-3.
Находим знаки производной в промежутках между критическими точками.
x = -4 -3 0 1 2
y' = -0,118343 0 0,48 0 -0,118343 .
Как видим, в точке х = -3 минимум функции, а в точке х = 1 - максимум.
Находим значения функции в этих точках.
у(-3) = (-2(9+3))/(9-6+5) = -24/8 = -3.
у(1) = (-2(1+3))/(1+2+5) = -8/8 = -1.
На заданном промежутке [-5; 1] значение функции у(1) = -1 является максимальным, а у(-3) =-3 минимальным.
а. 50 м² Арман очистил за 10 минут
б. 15 пакетов потребуется, чтобы расфасовать 150 кг гречки по 10 кг в каждый
Пошаговое объяснение:
а. Одна сотка представляет собой квадрат 10 метров на 10 метров, следовательно, 1 сотка = 100 м²
Составим пропорцию:
100 м² - 20 минут
х м² - 10 минут
х = 100 * 10 : 20 = 1000 : 20 = 50 м² Арман очистил за 10 минут
б. 50 : 10 = по 5 (кг) гречки расфасовали в каждый пакет из 10.
150 : (5 + 5) = 150 : 10 = 15 (пакетов) потребуется, чтобы расфасовать 150 кг гречки по 10 кг в каждый
540·0,8 = 432 (тг) - цена после 2-го снижения.
432· 3= 1296 (тг) - стоимость трех метров ткани по последней цене.