Изучая математику,мы проходим отношения чисел и величин.Одно число может быть меньше или больше другого,но для сравнения этого бывает недостаточно.Для решения практических задач нам необходимо знать,во сколько раз или на сколько одно число больше или меньше другого.
На сколько единиц одно число больше или меньше другого -это разностное сравнение.Для разносного сравнения необходимо из большего числа вычесть меньшее.
Во сколько раз одно число больше или меньше другого -это кратное сравнение.Для кратного сравнения необходимо большее число разделить на меньшее.
Пример:
На сколько 6-ть больше 3-х?Вычисляем: 6-3=3 ,получается 6-ть больше 3-х на 3 единицы.Это разностное сравнение.
Во сколько раз 6-ть больше 3-х?Вычисляем: 6:3=2 ,получается 6-ть больше 3-х в два раза.Это кратное сравнение .
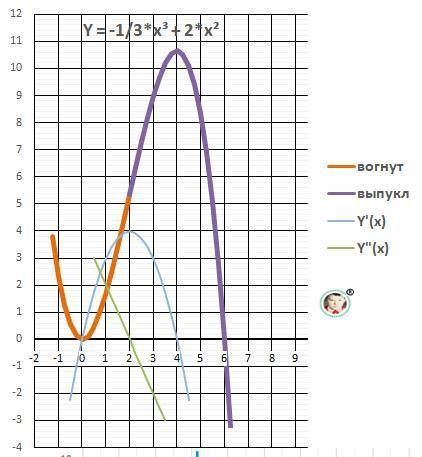
Дано: y(x) = 2*x² - 1/3*x³
Найти экстремумы.
Пошаговое объяснение - оно больше чем требует задача, но нужно для построения графика - лишнее удалить.
1. Область определения D(y) ∈ R, Х∈(-∞;+∞) - непрерывная , гладкая.
2. Пересечение с осью OХ.
Разложим многочлен на множители. Y=x²*(x-6) = 0.
Нули функции: Х₁ =0, Х₂ =0, Х₃ =6
3. Пересечение с осью OY. Y(0) = 0.
4. Интервалы знакопостоянства.
Положительная - Y(x)≥0 X∈(-∞;0]U[0;6]
Отрицательная - Y(x)<0 X∈[6;+∞)
5. Исследование на чётность.
В полиноме есть и чётные и нечётные степени - функция общего вида.
6. Первая производная. Y'(x) = -x² + 4*x = -х*(х-4) = 0
Корни Y'(x)=0. Х₄ =4 Х₅=0
7. Локальные экстремумы.
Максимум - Ymax(4) = 10 2/3 - ответ. (≈10,7)
Минимум - Ymin(0) = 0 - ответ.
8. Интервалы возрастания и убывания.
Убывает Х∈(-∞;0;]U[6;+∞) ,возрастает - Х∈[6;0]
12. Вторая производная - Y"(x) = -2*x +4 = -2*(х-2) = 0
Корень производной - точка перегиба - Х₆=2
13. Вогнутая “ложка» Х∈(-∞; Х₆ = 2]
Выпуклая – «горка» Х∈[Х₆ = 2; +∞).
14. График в приложении.
A∩B=N\{6n-5,n∈N}\{6n-1,n∈N}≡{6n;6n+2;6n+3;6n+4, n∈N}