Каноническое уравнение эллипса имеет вид:
(x²/a²) + (y²/b²) = 1.
Для того чтобы найти полуоси эллипса, подставим координаты точек M1(4 ; 4√5/5) и M2(0; 6) в уравнение эллипса.
(16/a²) + ((16/5)/b²) = 1.
(0/a²) + (36/b²) = 1.
Сделаем замену: (1/a²) = t, (1/b²) = u.
Получим: 16t + (16/5)u = 1.
0t + 36u = 1, отсюда u = 1/36, а b= +-6.
Подставим u в первое уравнение.
16t + ((16*1)*(5*36)) = 1, откуда получаем t = 41/(16*45).
Получаем a = +-(12√5/√41) ≈ +-4,190582.
ответ. Каноническое уравнение эллипса имеет вид: (x²/((12√5/√41)²) + (y²/6²) = 1.
Во вложениях дан рисунок эллипса и его параметры.
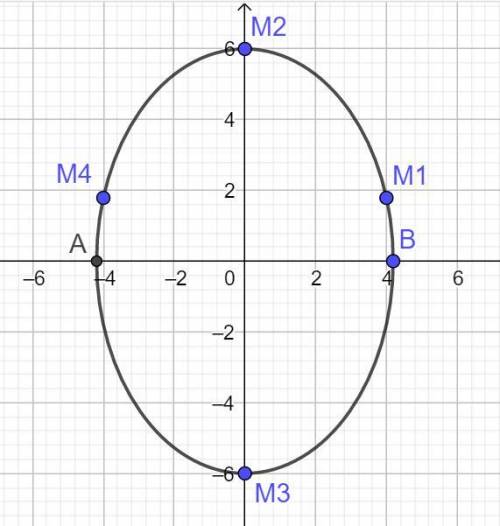
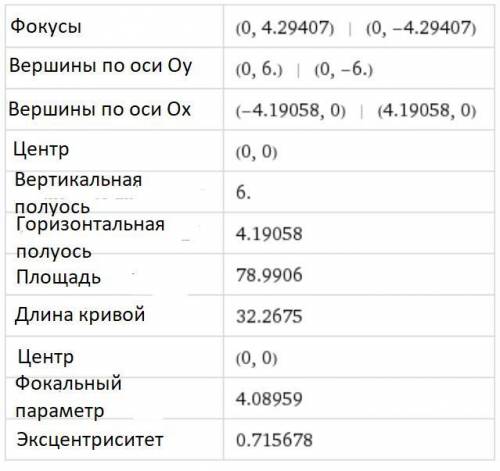
Пошаговое объяснение:
выпишем наименьшие по модулю углы для каждого пункта
а) при n = 0 |α| = 30, при n > 0 |α| ≥ 390 и при n < 0 |α| ≥ 330
б) при n = -1 |α| = 90, при n > -1 |α| ≥ 270 и при n < -1 |α| ≥ 450
в) при n = 0 |α| = 120, при n > 0 |α| ≥ 240 и при n < 0 |α| ≥ 480
г) при n = 1 |α| = 90, при n > 1 |α| ≥ 450 и при n < 1 |α| ≥ 270
д) при n = -1 |α| = 40, при n > -1 |α| ≥ 400 и при n < -1 |α| ≥ 320
е) при n = 2 |α| = 20, при n > 2 |α| ≥ 380 и при n < 2 |α| ≥ 340
если нужно выбрать наименьший среди всех пунктов, то это
е) при n = 2 |α| = 20, при n > 2 |α| ≥ 380 и при n < 2 |α| ≥ 340
1050/15=70
вс