Пошаговое объяснение:
Y = F'(Xo)*(x - Xo) + F(Xo) - формула касательной.
Находим наклон заданной прямой.
4*х + 4*у - 7 = 0
у = - х + 7/4 = k*x+ b
И так - наклон касательной - k = -1.
Находим производную функции.
F'(x) = 6*x² - 6*x - 1 = k = -1 - одинаковый наклон у касательной и той прямой.
F'(x) = 6*x²+ 6x = 6*x*(x-1) = 0
Две точки касания. Хо = 0 и Хо = 1.
Подставив в уравнение касательной получаем:
Вычисляем в точке Хо = 1.
F'(1) = 6 -6 + -1 = -1 - производная
F(1) = 2 -3 -1 + 2 = 0 - функция.
Записываем уравнения прямой.
Y = -1*(x - 1) + (0) = -x + 1 - уравнение касательной - ОТВЕТ
Вычисляем в точке Хо = 0.
F'(0) = 0 + 0 - 1 = -1 - производная
F(0) = 0 + 0 + 0 + 2 = 2 - функция.
Записываем уравнения прямой.
Y = -1*(x - 0) + (2) = - x + 2 - уравнение касательной - ОТВЕТ
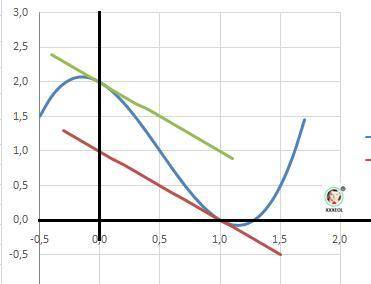
Рисунок с графиком функции и двумя касательными в приложении.
ДВЕ касательных с одинаковым наклоном.
Пошаговое объяснение:
Приравниваем и получаем квадратное уравнение.
1/5*x² = 20 - 3*x
y = 0,2*x²+3*x+-20 - квадратное уравнение.
a*x² + b*x + c = 0 Вычисляем дискриминант - D.
D = b² - 4*a*c = 3² - 4*(0,2)*(-20) = 25 - дискриминант. √D = 5.
Вычисляем корни уравнения.
x₁ = (-b+√D)/(2*a) = (-3+5)/(2*0,2) = 2/0,4 = 5 - первый корень
x₂ = (-b-√D)/(2*a) = (-3-5)/(2*0,2) = -8/0,4 = -20 - второй корень
5 и -20 - корни уравнения.
Вычисляем ординаты точек пересечения.
y(5) = 20 - 3*5 = 5 и y(-20) = 20 - 3*(-20) = 80.
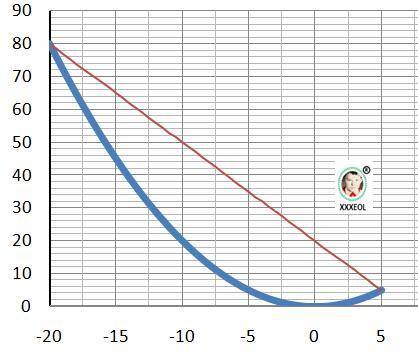
ОТВЕТ: (-20;80) и (5;5) - точки пересечения.
Рисунок к задаче в приложении.
1)43-34=9
2)23×2=46
3)9-46=-37
4)-37+12=-25
5)-25-65=-90