ответ:
книга под жепу ( рисковый вариант)
шпоры ( это если тебе сложно запомить какие-либо формулы и т.д.) просто запиши, что не знаешь где угодно, хоть на бутылке воды, или засунь бумажку в прозрачную ручку, можно и на теле написать.
самый лучший способ просто запомнить то, что тебе нужно, отпрситься в тубз и списать там с телефона, либо, если у вас перед конрольной забрали телефоны, так можно воспользоваться большой шпорой, которую палевно доставать. еще можно придумать какой-то извращенный способ, по типу: попросить кого-то позвонить во время контрольной, а потом сказать, учителю, что это важно и выйти.
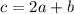
Пошаговое объяснение:
Базис. Векторы a и b образуют базис, поскольку на плоскости (у векторов по две координаты) любые два линейно независимых вектора образуют базис (поскольку пространство двумерно), а линейная независимость на плоскости эквивалентна условию, что векторы непараллельны, т.е. их координаты непропорциональны. Впрочем, можно подойти и формально, записав линейную комбинацию векторов a и b, а также приравняв её к нулю:
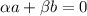
![\left[\begin{array}{cc}3&1\\5&-7\end{array}\right] * \left[\begin{array}{c}\alpha \\\beta \end{array}\right] = \left[\begin{array}{c}0\\0 \end{array}\right]](/tpl/images/4789/5603/bdaee.png)
где 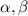 - числа. В силу того, что определитель матрицы векторов не равен нулю (матрица невырожденная), существует только нулевое решение, что означает линейную независимость векторов a и b.
- числа. В силу того, что определитель матрицы векторов не равен нулю (матрица невырожденная), существует только нулевое решение, что означает линейную независимость векторов a и b.
Разложение. Чтобы найти разложение вектора c по базису, приравняем линейную комбинацию векторов a и b к вектору c:
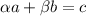
![\left[\begin{array}{cc}3&1\\5&-7\end{array}\right] * \left[\begin{array}{c}\alpha \\\beta \end{array}\right] = \left[\begin{array}{c}7\\3 \end{array}\right]](/tpl/images/4789/5603/5ff81.png)
Домножим левую и правую часть слева на обратную матрицу коэффициентов векторов:
![E*\left[\begin{array}{c}\alpha \\\beta \end{array}\right] =\left[\begin{array}{cc}3&1\\5&-7\end{array}\right]^{-1} * \left[\begin{array}{c}7\\3 \end{array}\right]](/tpl/images/4789/5603/30300.png)
Е - единичная матрица, можно опустить (получается при перемножении матрицы и обратной к ней).
![\left[\begin{array}{cc}3&1\\5&-7\end{array}\right]^{-1} = \left[\begin{array}{cc}\frac{7}{26} &\frac{1}{26} \\\frac{5}{26} &-\frac{3}{26} \end{array}\right]](/tpl/images/4789/5603/2cc1b.png)
![\left[\begin{array}{cc}3&1\\5&-7\end{array}\right]^{-1} * \left[\begin{array}{c}7\\3 \end{array}\right] = \left[\begin{array}{cc}\frac{7}{26} &\frac{1}{26} \\\frac{5}{26} &-\frac{3}{26} \end{array}\right]* \left[\begin{array}{c}7\\3 \end{array}\right] = \left[\begin{array}{c}2\\1\end{array}\right] = \left[\begin{array}{c}\alpha \\\beta \end{array}\right]](/tpl/images/4789/5603/ede93.png)
Итак,
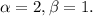
Значит, 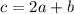 .
.
Прямой проверкой можно убедиться в правильности ответа:
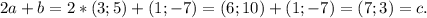
32:4=8 книг на одном столе
9-8=1