Математика: Вырази в килограммах 5 тонны 12тонны4т600кг

Пошаговое объяснение:1)2)3)для вычисления обратной матрицы запишем матрицу А, дописав к ней справа единичную матрицу:теперь чтобы найти обратную матрицу, преобразуем левую часть полученной матрицы в единичную.1-ую строку делим на -31 строку * 5 к 2ой добавляем 1 строку2-ую строку делим на и последнее 2ую * (2/3) и к 1 строке добавляем 2уюи вот 4)определитель матрицы А:∆A = 1*1 - 2*1 = -1nак как A невырожденная матрица, то существует обратная матрица A⁻¹Умножим справа обе части уравнения на A⁻¹:...

Вырази в килограммах 5 тонны 12тонны4т600кг

👇

Увидеть ответ

Ответ:

electreheart

25.03.2020

5 тонн = 5000 кг
12 тонн = 12000 кг
4тонны600 кг = 4600 кг
так как 1тонна = 1000 кг

4,6(90 оценок)

Ответ:

хината19

25.03.2020

1. 5000 кг
2.12000кг
3.4600кг
за то, что дал подзаработать )))

4,4(16 оценок)

Открыть все ответы

Ответ:

Maria325784

25.03.2020

ответ:

f(x) = -x^3+3x^2

1) область определения:

d(f): x принадлежит

2) четность/нечетность:

f(-x) = x^3+3x^2 - не является четной и нечетной

3) непрерывность:

функция непрерывна на всей области определения.

4) точки пересечения с осями координат:

ox: y=0 a(0,0), b(3,0)

oy: x=0 c(0,0)

5) асимптоты:

горизонтальная: нет

наклонная: y = kx+b, - нет

вертикальная: нет, т.к. нет точек разрыва

6) экстремум:

f'(x) = -3x^2+6x = -3x(x-2)

f'(x) = 0 при x = 0 или x = 2

- + -

..>

0 2 x

x=0 - точка минимума f(0) = 0 - наименьшее значение

x = 2 - точка максимума f(2) = 4 - наибольшее значение

7) выпуклость:

f''(x) = -6x+6

f''(x) = 0 при x = 1

+ -

.> x

при х график функции имеет выпуклость вниз,

при х - вверх

4,4(48 оценок)

Ответ:

ДашаСалина

25.03.2020

Пошаговое объяснение:

$\left[\begin{array}{ccc}3&2&1\\0&1&2\\\end{array}\right] *\left[\begin{array}{ccc}1\\2\\3\end{array}\right]=c$

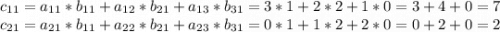
$c_{11} = a_{11} *b_{11} + a_{12}*b_{21} + a_{13}*b_{31} = 3*1 + 2*2 + 1 *0 = 3 + 4 + 0 = 7\\c_{21} = a_{21}* b_{11} + a_{22}* b_{21} + a_{23} *b_{31} = 0*1 + 1*2 + 2*0 = 0 + 2 + 0 = 2$

$c=\left[\begin{array}{ccc}7\\2\\\end{array}\right]$

$\left[\begin{array}{ccc}3&5\\6&1\\\end{array}\right] *\left[\begin{array}{ccc}2&1\\-3&2\\\end{array}\right] =c$

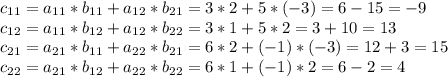
$c_{11} = a_{11}*b_{11} + a_{12}*b_{21} = 3* 2 + 5 *(-3) = 6 - 15 = -9\\c_{12} = a_{11}*b_{12} + a_{12}*b_{22} = 3 *1 + 5*2 = 3 + 10 = 13\\c_{21} = a_{21}*b_{11} + a_{22}*b_{21} = 6*2 + (-1)*(-3) = 12 + 3 = 15\\c_{22} = a_{21}*b_{12} + a_{22} * b_{22} = 6*1 + (-1)*2 = 6 - 2 = 4$

$c= \left[\begin{array}{ccc}-9&13\\15&4\\\end{array}\right]$

$A=\left[\begin{array}{ccc}-3&2\\5&-4\\\end{array}\right]$

для вычисления обратной матрицы запишем матрицу А, дописав к ней справа единичную матрицу:

$\left[\begin{array}{cccc}-3&2&1&0\\5&-4&0 &1\\\end{array}\right]$

теперь чтобы найти обратную матрицу, преобразуем левую часть полученной матрицы в единичную.

1-ую строку делим на -3

$\left[\begin{array}{cccc}1&-2/3&-1/3&0\\-5&4&0&1\\\end{array}\right]$

1 строку * 5 к 2ой добавляем 1 строку

$\left[\begin{array}{cccc}-1&-2/3&-1/3&0\\0&-7\frac{1}{3} &-1\frac{2}{3} &1\\\end{array}\right]$

2-ую строку делим на 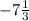$-7\frac{1}{3}$

$\left[\begin{array}{cccc}1&-2/3&-1/3&0\\0&1&5/22&-3/22\\\end{array}\right]$

и последнее 2ую * (2/3) и к 1 строке добавляем 2ую

$\left[\begin{array}{cccc}1&0&-2/11&-1/11\\0&1&5/22&-3/22\\\end{array}\right]$

и вот

$A^{-1}=\left[\begin{array}{ccc}-2/11&-1/11\\5/22&-3/22\\\end{array}\right]$

определитель матрицы А:

∆A = 1*1 - 2*1 = -1

nак как A невырожденная матрица, то существует обратная матрица A⁻¹

Умножим справа обе части уравнения на A⁻¹: X·A·A⁻¹ = B·A-1, откуда находим, что X = B·A⁻¹

найдем обратную матрицу A⁻¹.

транспонированная матрица

$A^T=\left[\begin{array}{ccc}1&2\\1&1\\\end{array}\right]$

aлгебраические дополнения

A₁₁ = (-1)¹⁺¹ *1 = 1; A₁₂ = (-1)¹⁺² *1 = -1;

A₂₁ = (-1)²⁺¹ *2 = -2; A₂₂ = (-1)²⁺² *1 = 1;

обратная матрица

$A^{-1}=\left[\begin{array}{ccc}1&-1\\-2&1\\\end{array}\right]$

тогда

$X=\left[\begin{array}{ccc}3&2\\-1&3&\\\end{array}\right] *\frac{1}{-1} \left[\begin{array}{ccc}1&-1\\-2&1\\\end{array}\right] =\left[\begin{array}{ccc}1&1\\7&-4\\\end{array}\right]$