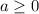
Пошаговое объяснение:
Рассмотрим 2 случая:
1-й случай: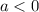 
.
Заметим, что тогда дискриминант больше 0
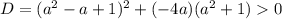так как
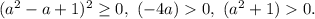
Значит уравнение имеет вещественные корни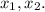 
По теореме Виета:
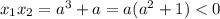, значит 
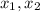-- разных знаков, то есть лежат по разные стороны от нуля. Что не удовлетваряет требованиям задачи. Значит никакие 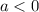не подходят.
2-й случай: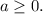 
Рассмотрим 2 подслучая:
2.1) оказалось, что дискриминант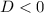 
.
Тогда уравнение не имеет положительных корней (потому что оно не имеет вещественных корней).
2.2) оказалось, что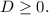 
Тогда уравнение имеет корни (возможно, кратные). Обозначим их 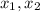. Заметим, что эти корни одного знака, так как их произведение (по теореме Виета):
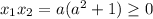. То есть они лежат по одну сторону от нуля. Чтобы понять по какую сторону от 0 они лежат, посмотрим на их сумму и опять воспользуемся теоремой Виета:
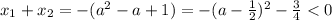, значит оба корня 
.
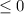Это значит, что все 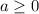подходят.
4. Найдите наименьшее значение функции y =12cosx +5sinx.
A) -5 B) -12 С) -13 D) 5 E) 12
5. Укажите ограниченную функцию :
A) y =tgx B) y =2/sinx С) y=3+cosx D) y =ctgx E) y =4 / cosx
6. Сравните числа a =sin10° , b=cos10° , c = ctg10°.
A) b < c <a B) c < a <b С) b <a < c D) a < c < b E) a < b <c
- - - - - - -
ответ: 4. С) -13 , 5. C) y=3+cosx , 6. E) a < b < c
Пошаговое объяснение:
4. y =12cosx +5sinx ⇔ y =13cos( x - arc(12/13) ) ⇒ min y = - 13 .
- - - - - - -
5. y=3+cosx - 2 ≤ 3+cosx ≤ 4
A) y =tgx B) y =2/sinx С) y=3+cosx D) y =ctgx E) y =4 / cosx
- - - - - - -
6. sin10 °< cos10° < ctg10° → E) a < b < c
Если 0° ≤ α ≤ 45 ° , т о :
sinα возрастает (↑) 0 ≤sinα ≤ 1/√2 ;
cosα убывает (↓) от 1 до 1/√2 ;
сtgα =coosα/ sinα убывает (↓) от +∞ до 1 .
* * *P.S. метод вс аргумента
* * *P.S. √ (12²+5²)=√ (144+25)=√ 169 = 13 ; (12/13)²+(5/12)² =1
y =12cosx +5sinx = 13( cosx (12 /13) +sinx *(5/12) ) = || 12 /13=cosφ ) ; 5/13=Sinφ ||
= 13( cosx *cosφ +sinx *Sinφ ) = 13cos(x- φ) ; φ =arc cos( 12 /13) . * * *
780-430=350
ответ: 350 маленьких пакетов