
1) Если х < 0, то левая часть неотрицательна в силу модуля, правая - отрицательна. Верно всегда, в ответ. 2) Если х = 0, то 30 >= 0 - верно. 3) Если х > 0, то можно возвести обе части в квадрат и представить это в виде разности квадратов:
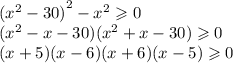
Методом интервалов при х > 0: х принадлежит (0;5] U [6; + беск.)
В итоге получаем ответ: ( - беск. ; 5 ] U [ 6 ; + беск. ). Не являются решением данного неравенства х принадлежит (5;6), но в этот интервал не входят целые числа, поэтому их количество равно 0
ответ: 0.
1107
Пошаговое объяснение:
т.к. у нас два сундук с четным количеством монет и два с нечетным, а за операцию каждый сундук меняет свою четность, то всегда будет два "нечетных" сундука
так как на одной итерации мы добавляем в три из четырех сундуков монеты, то только в одном сундуке мы можем добиться 0
значит, с учетом двух утверждений картина с наибольшим количеством монет могла выглядеть следующим образом: 0 1 1 1108
на предыдущем шаге должно было быть 3 0 0 1107 - но такого быть не могло, согласно утверждениям выше
следующий вариант, где монет меньше, чем 1108, это 1107
этого варианта достичь можно, пользуясь следующим алгоритмом:
четвертый сундук не трогаем, а с остальными повторяем следующую операцию:
берем сундук с наибольшим количеством монет и проводим операцию столько раз, сколько нужно, чтобы в сундуке осталось меньше трех монет
выглядит это так:
111 222 333 444
222 333 0 555
333 0 111 666
0 111 222 777
74 185 0 851
135 2 61 912
0 47 106 957
35 82 1 992
62 1 28 1019
2 21 48 1039
18 37 0 1055
30 1 12 1067
0 11 22 1077
7 18 1 1084
13 0 7 1090
1 4 11 1094
4 7 2 1097
6 1 4 1099
0 3 6 1101
2 5 0 1103
3 2 1 1104
0 3 2 1105
1 0 3 1106
2 1 0 1107
и он возьмет себе 1107 монет
8 - 3 = 5 (м/с) скорость первого
2) 738 ÷(14 - 5)= 82 (км/ч)
3) 432÷9 = 48(км/ч) скорость поезда
432÷6 = 72(км/ ч) нужная скорость
72 - 48 = 20 (км/ч) должен увеличить скорость