. Условие, что выражение равно единице, можно записать так:
(100 + n)k(100 - n)l = 100k + l. Так как правая часть четна, то и левая часть должна быть четна, значит, n четно. Аналогично, левая часть делится на 5, значит, n делится на 5. Значит, n делится на 10. Можно перебрать все 9 возможных вариантов: n = 10, 20, ..., 90. Например, если n = 10, то левая часть делится на 11, что невозможно.Можно обойтись без перебора: пусть n не делится на 25. Тогда числа 100 - n и 100 + n тоже не делятся на 25. Значит, пятерка входит в разложение левой части на простые множители ровно k + l раз. Но она входит в разложение правой части 2(k + l ) раз -- противоречие. Итак, n делится на 25. Аналогично доказывается, что n делится на 4. Но тогда n делится на 100, что невозможно, ибо 0 < n < 100.
1. в) -5:2<0
-2.5<0
2. a) -8*9=-72
б) -8,35*100 = -(8,35*100) = -835
в) -36:4 = -9
г) -60,4 : (-0,4) = 60,4 : 0,4 = 151
3. а) 10х=-5
х= -  = -
= -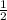
б) х:(-0,2) = 8
х:(-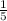 ) = 8
) = 8
-х*5 = 8
-5х = 8
х = -
4. а) -6,2*3 = -18,6
б) -19,68 : (-0,8) = 19,68 : 0,8 = 24,6
в) 16,32: (-16) = -(16,32: 16) = -1,02
5. а) 0,5*(-36)*2 = -(0,5*36*2)= -(18*2) = -36
б) -500*37,38(-2)*0,1 = 18690*2*0,1=1869*2=2
6. (0,8-2,86:2,6)*(3,04-7,02) = (0,8-1,43)(-3,98) = -0,63*(-3,98) = 2,5
7. |-3x-1.5| = 0.5
-3x-1.5 = 0.5 -3x-1.5 = -0.5
-3x= 0.5 + 1.5 -3x = -0.5 + 1.5
-3x = 2 -3x = 1
x= - 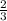 x = -
x = -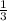
3,2м*1м*0,85м=2,72м^3 => 2720 литров