Алгоритм.
1. найдем производную функции f'(x)=(2x⁶-5x⁴)'=12x⁵-20x³=
4x³(3x²-5)
2. Найдем критические точки. 4x³(3x²-5)=0, х=0; 3х²=5; х=±√(5/3)
3. Решим неравенство 4x³(3x²-5)≥0, установив промежутки возрастания и убывания.
-√(5/3)0√(5/3)
- + - +
функция убывает при х∈ (-∞;-√(5/3)] и при х∈ [0;√(5/3)]
функция возрастает при х∈[-√(5/3);0] и при х∈ [√(5/3);+∞)
х= -√(5/3); х=√(5/3) -точки минимума, т.к. при переходе через них производная меняет знак с минуса на плюс.
х=0- точка максимума, т.к. при переходе через нее производная меняет знак с плюса на минус.
Если существует предел 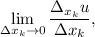 то этот предел называется частной производной от функции
то этот предел называется частной производной от функции 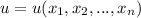 по переменной
по переменной 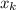 и обозначается
и обозначается 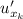 или
или 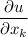
Для функции 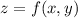 следует найти частные производные
следует найти частные производные 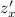 и
и 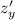
Для нахождения таких производных по данной переменной следует все переменные, кроме данной, считать константами (числами).
Например, для функции 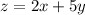 частной производной функции по переменной
частной производной функции по переменной  будет:
будет: 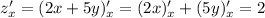 (считаем выражение
(считаем выражение 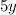 числовым, производная от которого равна нулю), и аналогично по переменной
числовым, производная от которого равна нулю), и аналогично по переменной 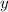 будет:
будет: 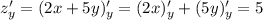
Для заданной функции 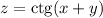 найдем частные производные
найдем частные производные 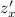 и
и 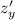
Воспользуемся формулой 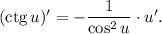
Имеем:
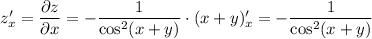
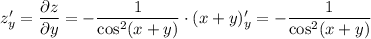
ответ: 
Наливаем 3 пригоршни
Выливаем во второй сосуд
Наливаем 3 пригоршни
Выливаем во второй сосуд
Наливаем 3 пригоршни
Выливаем во второй сосуд, у нас остаётся 1 пригоршня
Выливаем все из второго сосуда
Выливаем 1 пригоршню во второй сосуд
Наливаем 3 пригоршни
Выливаем во второй сосуд
Наливаем 3 пригоршни
Выливаем во второй сосуд