Вящике есть 30 прономерованых от 1 до 30 жетонов. какая вероятность того что номер наугад взятого жетона - id919854320220823 от Baidu 23.08.2022 17:57

Question

Математика: Вящике есть 30 прономерованых от 1 до 30 жетонов. какая вероятность того что номер наугад взятого жетона будет кратным числу 7?

Baidu · Accepted Answer

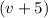Пусть первая труба пропускает литров. Тогда вторая (v+5) л. Если мы вычтем из более производительной трубы мене производительную, то получим время, которое требуется второй трубе, когда первая труба уже заполнила резервуар. Это время по условию равно 10 мин:

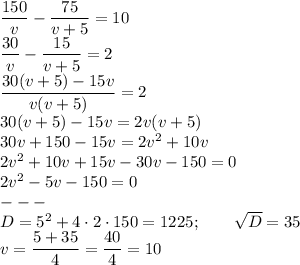
$\dfrac{150}{v}-\dfrac{75}{v+5}=10\\\dfrac{30}{v}-\dfrac{15}{v+5}=2\\\dfrac{30(v+5)-15v}{v(v+5)}=2\\30(v+5)-15v=2v(v+5)\\30v+150-15v=2v^2+10v\\2v^2+10v+15v-30v-150=0\\2v^2-5v-150=0\\---\\D=5^2+4 \cdot2 \cdot 150=1225; \qquad \sqrt{D}=35\\v=\dfrac{5+35}{4}=\dfrac{40}{4}=10$

Второй корень явно отрицателен, поэтому он нам не подходит, т. к. скорость/производительность — величина положительная.

Тогда вторая труба по условию пропускает 10+5=15 л/мин

ответ: 1-я труба — 10 л/мин, 2-я труба — 15 л/мин.

Проверка: первая труба заполнит первый резервуар за 150:10=15 мин.

Вторая труба за 75:15=5 мин. Мы видим, что первый резервуар заполняется на 10 минут дольше, что и требовалось доказать.

Вящике есть 30 прономерованых от 1 до 30 жетонов. какая вероятность того что номер наугад взятого жетона будет кратным числу 7?

MOGZ ответил