Пошаговое объяснение:
а)
<вета=30 градусов
Боковая сторона b=10
S=1/2×a×h
а - основание
h - высота
cos<вета=а/2 : b
a/2=b×cos30=10×(корень 3/2)=
=5корень3
а=5корень3 ×2=10 корень3
Катет лежащий против угла 30 равен половине гипотенузе :
h=1/2×b=1/2×10=5
S=1/2×10корень3 ×5=25 корень3 (ед^2)
Р=а+2b
P=10 корень3 +2×10=10корень3 +20 (ед)
б)
<вета=45 градусов
b=8
a - основание
h - высота
cos <вета=а/2 : b
a/2=b×cos45=8×(корень2 /2)=4корень2
а=4корень2×2=8корень2
h=a/2=4 корень 2, т. к тр-к равнобедренный
S=1/2×a×h
S=1/2×8корень2 ×4корень2 =32 (ед^2)
Р=а+2b
P=8корень2 +2×8=8корень2+16 (ед)
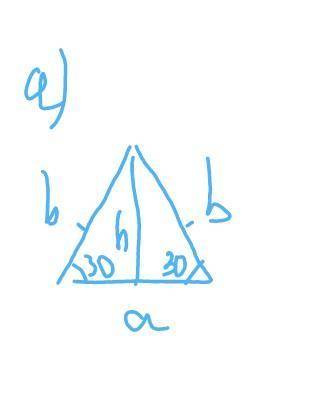
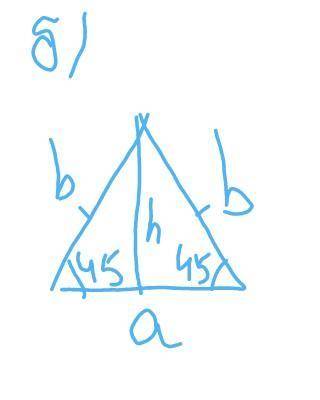
Формулы: A b/c = a*c+b/c
a/b * c/d = a*c/b*d
1 1/4 * 1 1/5 = 5/4 * 6/5 = 5*6/4*5, сокращаем на 5: = 6/4 = 3/2 = 1 1/2
2 1/2 * 2 4/5 = 5/2 * 14/5 = 70/10=7
2 2/7 * 1 1/8 = 16/7 * 9/8, сокращаем 16 в числителе и 8 в знаменателе (на 8): =2/7 * 9/1=18/7 = 2 4/7
1 3/5 * 7 1/2 = 8/5 * 15/2, сокращаем 15 в числ. и 5 в зн.(делим на 5): = 8/1*3/2 = 24/2= 12
2 1/7 * 2 2/15 = 15/7*32/15, сокращаем 15: 1/7 * 32/1 = 32/7= 4 4/7
2 2/9 * 2 19/40 = 20/9 * 99/40, сокращаем 99 и 9(на 9) и 20 и 40(на 20): = 1/1 * 11/2 = 11/2 = 5 1/2
Сокращение, когда делишь числитель и знаменатель на одинаковые числа.
Находим производную, приравниваем её к 0, найденные точки выставляются на числовой прямой; к ним добавляются те точки, в которых производная не определена.
На промежутках находим знаки производной
Где производная положительна - функция возрастает, где отрицательна - там убывает. Точки, в которых происходит смена знака и есть точки экстремума - где производная с плюса меняется на минус - точка максимума, а где с минуса на плюс - точки минимума.
Производная равна: y' = 3x^2+10x+7.
Приравниваем её нулю:
3x^2+10x+7 = 0.
Квадратное уравнение, решаем относительно x:
Ищем дискриминант:
D=10^2-4*3*7=100-4*3*7=100-12*7=100-84=16;
Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√16-10)/(2*3)=(4-10)/(2*3)=-6/(2*3)=-6/6=-1;
x_2=(-√16-10)/(2*3)=(-4-10)/(2*3)=-14/(2*3)=-14/6 = -(7/3) ≈ -2.33333.
x = -3 -2,33333 -2 -1 0y' = 4 0 -1 0 7
· Минимум функции в точке: х = -1,
· Максимум функции в точке: х = -7/3.