Сколько нужно бросить игральных костей , чтобы вероятностью , не меньшей 0,8 , ни на одной из выпавших граней не появилась цифра 1 ?

👇

Ответ:

kamilla202

03.11.2020

Вероятность того, что после первого броска не выпадет единица равна 5/6. Вероятность того, что единица не выпадет оба раза (т.е после второго броска) равна 5/6×5/6. Вероятность того, что после n бросков не появится единица равна (5/6)ⁿ; нужно найти такое n, что (5/6)ⁿ ≥ 0,8; Таким образом, при n≥0, n может быть равен только 1. Значит нужно бросить лишь одну кость. При двух костях вероятность 25/36 < 0,8

4,7(88 оценок)

Открыть все ответы

Ответ:

aidafarhadova

03.11.2020

Упрощаем выражения 1) -4а • 5 = -4 • 5а = -20а, коэффициент - это число (-20); 2) 8b • (-3) = 8 • (-3) • b = -24b, коэффициент - это число (-24); 3) (-5c) • 2 = (-5) • 2 • с = -10с, коэффициент - это число (-10); 4) 4x • (-3) = 4 • (-3)• х = - 12х, коэффициент - это число (-12); 5) 9y • (-5) = 9• (-5)у = -45у, коэффициент - это число (-45); 6) (-7m) • (-8) = 56 m, коэффициент - это число 56; 7) m • (-3) • (-5) = 15m, коэффициент - это число 15; 8) n • 7 • (-2) = -14n, коэффициент - это число (-14); 9) (-k) • 5 • (-3) = 15k, коэффициент - это число 15.

Пошаговое объяснение:

Упрощаем выражения 1) -4а • 5 = -4 • 5а = -20а, коэффициент - это число (-20);

2) 8b • (-3) = 8 • (-3) • b = -24b,

коэффициент - это число (-24); 3) (-5c) • 2 = (-5) • 2 • с = -10с

коэффициент - это число (-10); 4) 4x • (-3) = 4 • (-3)• х = - 12х,

коэффициент - это число (-12); 5) 9y • (-5) = 9• (-5)у = -45у,

коэффициент - это число (-45); 6) (-7m) • (-8) = 56 m,

коэффициент - это число 56; 7) m • (-3) • (-5) = 15m,

коэффициент - это число 15; 8) n • 7 • (-2) = -14n,

коэффициент - это число (-14); 9) (-k) • 5 • (-3) = 15k, коэффициент - это число 15.

4,8(49 оценок)

Ответ:

Василий2005

03.11.2020

точка A(1;-2) расположена вне окружности

Пошаговое объяснение:

Решим задание через определение степени точки относительно окружности

Степенью точки относительно данной окружности называется разность

${ d^{2}-R^{2}} ,$

d — расстояние от точки до центра окружности,

R — радиус окружности.

Точки имеют следуюющие степени в зависимости от расположения:

- вне окружности - положительную,

- внутри окружности - отрицательную,

- на окружности - нулевую.

Общее уравнение окружности задается уравнением

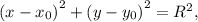
$\left(x-x_{0}\right)^{2}+\left(y-y_{0}\right)^{2}=R^{2},$

где (х0, у0) - координаты центра окружности

R - ее радиус.

В нашем случае:

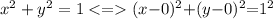
$x^2+y^2 = 1 < = (x{ - }0) {}^{2}{ +} (y{ -} 0) {}^{2}{ = } {1}^{2}$

Следовательно,

радиус окружности R = 1;

центр окружности O = О(0; 0)

Теперь вычислим степень точки A(1;-2) относительно этой окружности:

$A = A(1;-2); \: \: \: O =O(0;0); \: \: { R = 1} , \\ d=|AO|=\sqrt{(A_x-O_x)^2+(A_y-O_y)^2} \\ d = \sqrt{(1 - 0) {}^{2} + ( - 2 - 0) {}^{2} } = \\ = \sqrt{ {1}^{2} + ( - 2) {}^{2} \: } = \sqrt{1 + 4} = \sqrt{5} \\ {d}^{2} - {R}^{2} = ( \sqrt{5} )^{2} - {1}^{2} = 5 - 1 = 4 0$