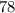км, а другой –
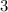раза больше, чем первый, то другой поезд 
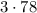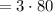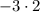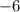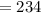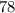км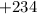 
км 
км 
км 
км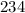 
км 
км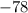. км 
км 
км.
км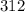 
км 
км.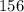
км ;
км .
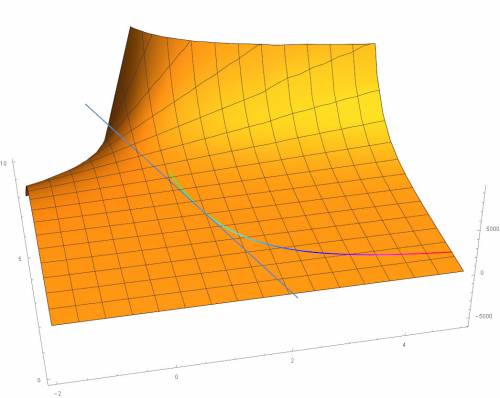
Для наглядности удобно провести некоторое соответствие с трехмерным пространством
Понятно что z(x,y) можно в нем изобразить как некоторую поверхность
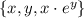
Точке (1,4) соответствует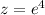 
, т.е. точка 
(*)
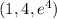Линию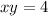 
удобнее записать как трехмерную кривую 
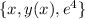, что будет пересекать поверхность z(x,y) при x=1
Запишем уравнение касательной к этой кривой в точке 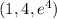, в качестве параметра берем переменную x
(#)
(вычисляется по аналогии с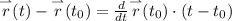 
)
В прикрепленном файле нарисована поверхность, кривая и касательная.
Зная уравнение касательной, построим единичный вектор в направлении убывания x:
Пусть x=0, тогда из (#) получим точку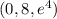 
Соотв. единичный вектор в направлении этой точки из (*) имеет вид
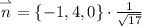
Понятно что z компонента никак не повлияет на значение производной по направлению, формально вектор можно записать как
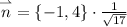
И, наконец, найдем искомую производную:
![grad[z(M_0)]\cdot\overset{\rightharpoonup }{n}=\left\{e^4,1 \cdot e^4\right\} \cdot \{-1,4\}\cdot\frac{1}{\sqrt{17} } = \frac{3 e^4}{\sqrt{17}} \approx 39.726](/tpl/images/0992/5590/2e9d7.png)
r=d/2=8мм=0.08 дм
l=50м=50*10дм=500дм
1 дм³=1л
V=πr²l=0,08²*500π дм³= 0.0064*500*π дм³≈3.2*3.14= 10,05 л