1.
Δ AA₁P~Δ MM₁P (AA₁||MM₁)
∠APA₁=∠MPM₁ как вертикальные
из подобия
AP:PM=5:8
AM=AP+PM=(5/8)PM+PM=(13/8)PM
AM=MB
MB=(13/8)PM
PB=PM+MB=PM+(13/8)PM=(21/8)PM
Δ MM₁P~Δ BB₁P (BB₁||MM₁)
MM₁:BB₁=PM:PB
BB₁=21
2.
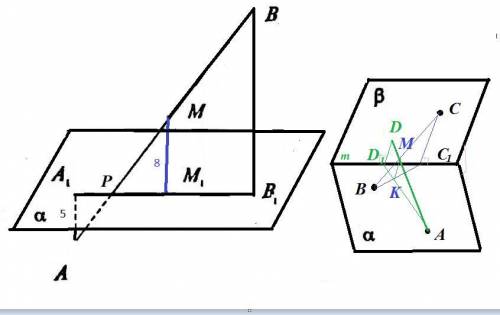
Пусть m- линия пересечения α и β
Проводим СС₁⊥m
Проекцией BC на пл. α является ВС₁
Пусть K - проекция точки пересечения BC и AD.
Проводим АК до пересечения с m, получаем точку D₁
проводим прямую через точку K || CC₁ , получаем точку M
Проводим прямую через точку D₁ перпендикулярно m, пересечение этой прямой с АМ - точка D
точка D - искомая точка.
функция непрерывна и принимает все значения от -∞ до +∞, но можно найти локальные максимум и минимум
y' = 3x² - 300 = 0
x² = 100
x = -10
x = 10
y(-10) = -1000 + 3000 + 5 = 2005 - максимум
y(10) = 1000 - 3000 + 5 = -1995 минимум
ответ: х = -10 - точка локального максимума