Производная равна 3х²+24х+36=0
х²+8х+12=0
D=64-48=16
х₁=(-8+4)\2=-2
х₂=(-8-4)\2=-6
-6∉[-5;-0,5]
-2∈[-5; -0,5]
Проверим знаки производной в [-5;-2) и в (-2;-0,5], это "-" и "+"⇒у(х) на первом интервале убывает, на втором возрастает ⇒х=-2 - точка минимума
у(-2)=(-2)³+12(-2)²+36(-2)+88=-8+48-72+88=-80+136=56
ответ : 56
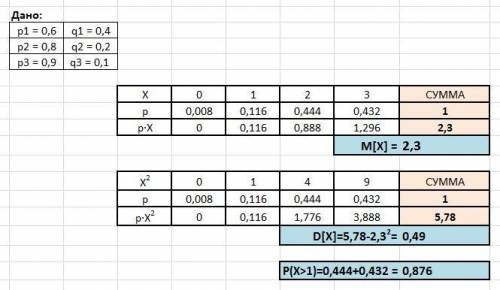
Решим задачу в Excel (см. приложение)
Необходимые пояснения:
Вероятность покупки (и не покупки):
p₁ = 0,6; q₁ = 1 - p₁ = 0,4
p₂ = 0,8; q₂ = 1 - p₂ = 0,2
p₃ = 0,9; q₂ = 1 - p₃ = 0,1.
Ряд распределения.
Число покупок:
X₀ = 0 - покупок не сделано;
X₁ = 1 - покупка сделана только одним покупателем;
X₂ = 2 - покупку сделали двое покупателей;
X₃ = 3 - покупку сделали все покупатели.
Функция распределения.
Всевозможные исходы:
P₀ = q₁·q₂·q₃ = 0,008;
P₁ = p₁·q₂·q₃ + q₁·p₂·q₃ + q₁·q₂·p₃ = 0,116;
P₂ = p₁·p₂·q₃ + p₁·q₂·p₃ + q₁·q₂·p₃ = 0,444;
P₃ = p₁·p₂·p₃ = 0,432.
Проверка:
0,008+0,116+0,444+0,432 = 1
Математическое ожидание:
M[X] = 0·0,008 + 1·0,116 + 2·0,444 + 3·0,432 = 2,3
Дисперсия:
D[X] = 0²·0,008 + 1²·0,116 + 2²·0,444 + 3²·0,432 - 2,3² = 0,49
Вероятность
P(x>1) = 0,444+0,432=0,876
а) 22° 30'; 45°; 112° 30'.
б) 59°, 60°, 61°.
Пошаговое объяснение:
а)
Будем считать, что в тексте задачи речь об углах, пропорциональных числам 1, 2 и 5.
∠А : ∠В : ∠С = 1 : 2 : 5.
Пусть в одной части х°, тогда
∠А = х°,
∠В = 2х°,
∠С = 5х°.
Зная, что сумма углов треугольника равна 180°, составим и решим уравнение:
х + 2х + 5х = 180
8х = 180
х = 22 1/2
∠А = 22 1/2° = 22° 30'.
∠В = 2•22 1/2° = 45°;
∠С = 5•22 1/2° = 112° 30'.
ответ: 22° 30'; 45°; 112° 30'.
б) Обозначим меньший угол треугольника за х°, тогда следующие за ним две градусные меры, выраженные целыми числами, равны (х+1)° и (х+2)°.
Зная, что сумма углов треугольника равна 180°, составим и решим уравнение:
х + х +1 + х + 2 = 180
3х = 180 - 3
3х = 177
х = 59
∠ 1 = 59°; ∠ 2 = 59° + 1° = 60°; ∠ 3 = 60° + 1° = 61°.
ответ: 59°, 60°, 61°.
Производная равна 3х²+24х+36=0
х²+8х+12=0
D=64-48=16
х₁=(-8+4)\2=-2
х₂=(-8-4)\2=-6
-6∉[-5;-0,5]
-2∈[-5; -0,5]
Проверим знаки производной в [-5;-2) и в (-2;-0,5], это "-" и "+"⇒у(х) на первом интервале убывает, на втором возрастает ⇒х=-2 - точка минимума
у(-2)=(-2)³+12(-2)²+36(-2)+88=-8+48-72+88=-80+136=56
ответ : 56