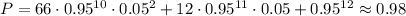Question

Решить при выпуске приборов на заводе 5% бывают недостаточно точными. берут наудачу 12 приборов. найти вероятность того, что из них не менее 10 будут точными.

Answer 1

Вероятность того, что при выпуске приборов на заводе будут точными равна 1-0,05=0,95.

Вероятность того, что при выпуске приборов на заводе будут 10 точных, равна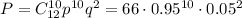 $P=C^{10}_{12}p^{10}q^2=66\cdot0.95^{10}\cdot 0.05^2$

Вероятность того, что при выпуске приборов на заводе будут 11 точных, равна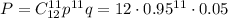 $P=C^{11}_{12}p^{11}q=12\cdot0.95^{11}\cdot 0.05$

Вероятность того, что при выпуске приборов на заводе будут 12 точных, равна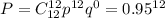 $P=C^{12}_{12}p^{12}q^0=0.95^{12}$

Искомая вер-ть: $P=66\cdot0.95^{10}\cdot 0.05^2+12\cdot0.95^{11}\cdot 0.05+0.95^{12}\approx0.98$