при нечётном количестве чисел в кругу сумма первого и последнего числа всегда будет чётной
Модуль "Алгебра"
Задание 1
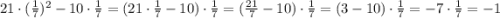
Задание 2

ответ: 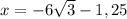
Задание 3
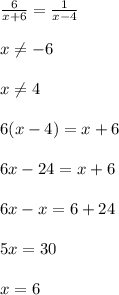
Правильный ответ №1.
Задание 4
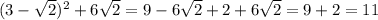
Задание 5
Обозначим скорость течения за 
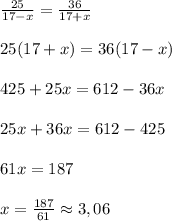
Модуль "Геометрия"
Задание 6
Первое утверждение неверно. Трапеция может быть обычной, равнобедренной или прямоугольной. Трапеция - четырёхугольник. И если все углы в четырёхугольнике равны, то это квадрат, а не трапеция.
Второе утверждение неверное, так как один из смежных углов является тупым, а второй острым.
Третье утверждение может быть верным, если речь идёт о прямоугольной трапеции.
Четвёртое утверждение неверно, так как один из смежных углов является тупым, а второй острым.
Для двух соседних четных или двух соседних нечетных ничего доказывать не нужно. Очевидно, что:
2n + 2(n+k) = 2(2n+k) - четное при любых n; k∈N, и
(2n - 1) + (2(n+k) - 1) = 2(2n+k) - 2 - четное при любых n; k∈N.
Допустим, что все числа написаны в максимально "неприятном" для нас порядке, - четные и нечетные числа чередуются. Возможны 2 варианта: первое число четное и первое число нечетное.
В первом случае рядом оказываются четные числа под номерами 1 и 7 (если первое число четное и равно 2n, то и седьмое также четное и равно 2(n + k). n; k∈N).
Во втором случае рядом оказываются нечетные числа под номерами 1 и 7 (если первое число нечетное и равно 2n - 1, то и седьмое число также нечетное и равно 2(n + k) - 1. n; k∈N).
Понятное дело, что сумма двух четных так же, как и сумма двух нечетных чисел, есть число четное:
2n + 2(n + k) = 2(2n + k) - четное при любых n; k∈N,
2n - 1 + 2(n + k) - 1 = 2(2n + k) - 2 - четное при любых n; k∈N.
Таким образом, при любом размещении семи натуральных чисел по кругу всегда найдутся два соседних, сумма которых четна.