Куб представляет собой многогранник у которого каждая грань представляет собой квадрат. Вычислим чему равна сумма площади граней куба, зная, что площадь одной грани равна 16 см². У куда всего 6 граней.
S = 6 * 16 = 96 см².
Вычислим чему равна длина одного ребра, зная, что площадь грани равна 16 см². Для этого мы должны извлечь квадратный корень от числа 16.
а = 4 см.
Объем куба равен произведению его длины на ширину и на высоту. Так как эти величины равны у куба, то есть объем равен:
V = 4 * 4 * 4 = 16 * 4 = 64 см³.
ответ: 96 см²; 64 см³.
Пошаговое объяснение:
Відповідь:
Покрокове пояснення:
а1 - проекція катета а на гіпотенузу
b1 - проекція катета b на гіпотенузу
a^2 = c*a1; b^2 c*b
а) c = 6 + 24 = 30 см
a^2 = 30*6 = 180
a =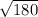 
= 6
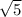см
b^2 = 30*24 = 720
b =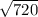 
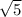= 12 см
б) c = 12 + 16 = 28
a^2 = 28*12 = 336
a =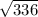 
= 16
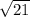см
b^2 = 28*16 = 448
b =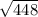 
= 16
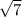см
в) c = 8 + 10 = 18 см
a^2 = 18*8 = 144
a =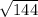 
= 12 см
b^2 = 18*10 = 180
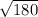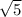b = = 6 см
г) c = 3 + 23 = 26
a^2 = 26*3 = 78
a =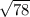 
см
b^2 = 26*23 = 598
b =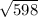 
см
Медиана базы трех чисел равна 28, то есть среди этих трех чисел медиана будет серединой: x, 28, y, где х - меньшее число и у - большее число.
Меньшее число меньше большего в 3 раза, то есть: Пусть х - меньшее число, тогда большее число: y = 3x. Среднее арифметическое трех чисел: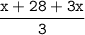
и равно, по условию, 28
Составим уравнение
То есть, выборка трех чисел имеет вид: 14; 28; 42. Осталось теперь определить наибольшую разность: y - x = 42 - 14 = 28.
ответ: 28.