Будем разбивать на несколько случаев.
1) Если из первой урны взяли 4 чёрных шара. Вероятность достать четыре чёрных шара равна 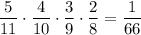 . Тогда во второй урне будет 3 белых и 9 черных шаров. Вероятность того, что среди трех отобранных шаров из второй урны окажутся все белые равна
. Тогда во второй урне будет 3 белых и 9 черных шаров. Вероятность того, что среди трех отобранных шаров из второй урны окажутся все белые равна  . По теореме умножения
. По теореме умножения 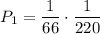
2) Если из первой урны взяли 1 белый шар и 3 чёрных. Вероятность такого события равна 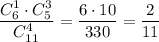 . Тогда во второй урне будет 4 белых и 8 черных шаров. Вероятность того, что среди отобранных шаров из второй урны все белые равна
. Тогда во второй урне будет 4 белых и 8 черных шаров. Вероятность того, что среди отобранных шаров из второй урны все белые равна 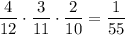 . По теореме умножения:
. По теореме умножения: 
3) Из первой урны взяли 2 белых шара и 2 чёрных. Вероятность такого события: 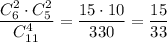 . Во второй урне будет 5 белых и 7 черных шаров. Вероятность того, что среди отобранных 3 шаров из второй урны все окажутся белыми равна
. Во второй урне будет 5 белых и 7 черных шаров. Вероятность того, что среди отобранных 3 шаров из второй урны все окажутся белыми равна 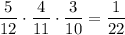 . По теореме умножения :
. По теореме умножения : 
4) Из первой урны взяли 3 белых шара и 1 чёрный шар. Вероятность достать 3 белых шара и 1 чёрный шар равна  . Во второй урне останется 6 белых и 6 чёрных шаров. Вероятность того, что среди отобранных шаров из второй урны окажутся все белыми равна
. Во второй урне останется 6 белых и 6 чёрных шаров. Вероятность того, что среди отобранных шаров из второй урны окажутся все белыми равна  . По теореме умножения:
. По теореме умножения: 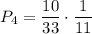
5) И, наконец, когда из первой урны урны взяли все четыре белых шаров. Вероятность такого события: 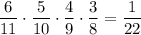 . Во второй урне остается 7 белых и 5 черных шаров. Вероятность того, что среди отобранных 3 шаров из второй урны окажутся все белыми равна
. Во второй урне остается 7 белых и 5 черных шаров. Вероятность того, что среди отобранных 3 шаров из второй урны окажутся все белыми равна 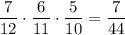 . По теореме умножения:
. По теореме умножения: 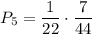
Итого, по теореме сложения:

Будем разбивать на несколько случаев.
1) Если из первой урны взяли 4 чёрных шара. Вероятность достать четыре чёрных шара равна 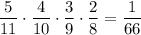 . Тогда во второй урне будет 3 белых и 9 черных шаров. Вероятность того, что среди трех отобранных шаров из второй урны окажутся все белые равна
. Тогда во второй урне будет 3 белых и 9 черных шаров. Вероятность того, что среди трех отобранных шаров из второй урны окажутся все белые равна  . По теореме умножения
. По теореме умножения 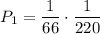
2) Если из первой урны взяли 1 белый шар и 3 чёрных. Вероятность такого события равна 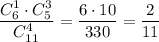 . Тогда во второй урне будет 4 белых и 8 черных шаров. Вероятность того, что среди отобранных шаров из второй урны все белые равна
. Тогда во второй урне будет 4 белых и 8 черных шаров. Вероятность того, что среди отобранных шаров из второй урны все белые равна 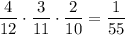 . По теореме умножения:
. По теореме умножения: 
3) Из первой урны взяли 2 белых шара и 2 чёрных. Вероятность такого события: 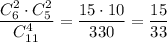 . Во второй урне будет 5 белых и 7 черных шаров. Вероятность того, что среди отобранных 3 шаров из второй урны все окажутся белыми равна
. Во второй урне будет 5 белых и 7 черных шаров. Вероятность того, что среди отобранных 3 шаров из второй урны все окажутся белыми равна 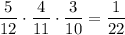 . По теореме умножения :
. По теореме умножения : 
4) Из первой урны взяли 3 белых шара и 1 чёрный шар. Вероятность достать 3 белых шара и 1 чёрный шар равна  . Во второй урне останется 6 белых и 6 чёрных шаров. Вероятность того, что среди отобранных шаров из второй урны окажутся все белыми равна
. Во второй урне останется 6 белых и 6 чёрных шаров. Вероятность того, что среди отобранных шаров из второй урны окажутся все белыми равна  . По теореме умножения:
. По теореме умножения: 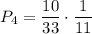
5) И, наконец, когда из первой урны урны взяли все четыре белых шаров. Вероятность такого события: 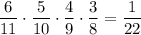 . Во второй урне остается 7 белых и 5 черных шаров. Вероятность того, что среди отобранных 3 шаров из второй урны окажутся все белыми равна
. Во второй урне остается 7 белых и 5 черных шаров. Вероятность того, что среди отобранных 3 шаров из второй урны окажутся все белыми равна 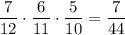 . По теореме умножения:
. По теореме умножения: 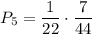
Итого, по теореме сложения:

7 684 : (99 595 + 36 + 369 - 96 164 + 6) * 52
1) 99 585 + 36 = 99 631
2) 99 631 + 369 = 100 000
3) 100 000 - 96 164 = 3 836
4) 3 836 +6 = 3 842
5) 7 684 : 3 842 = 2
6) 2 * 52 = 104
ответ: 104
14 056 - (42 103 + 14) : 3 + (18 710 - 18 708) · 45
1) 42 103 + 14 = 42 117
2) 18 710 - 18 708 = 2
3) 42 117 : 3 = 14 039
4) 2 * 45 = 90
5) 14 056 - 14 039 = 17
6) 17 + 90 = 107
ответ: 107
81 + 46 028 - (35 450 - 5 · 25) : 225 · 293
1) 25 * 5 = 125
2) 35 450 - 125 = 35 325
3) 35 325 : 225 = 157
4) 157 * 293 = 46 001
5) 81 + 46 028 = 46 109
6) 46 109 - 46 001 = 108
ответ: 108