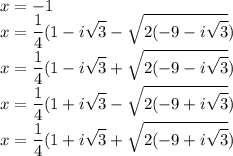
Пошаговое объяснение:
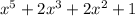
Подставим вместо х -1. Тогда получим
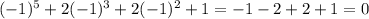
Тогда х = -1 корень данного многочлена. Тогда этот многочлен можно представить в виде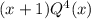 
, где Q - многочлен 4 степени. Найдём Q
Так как многочлен симметричный, то и Q будет симметричным. (это верно потому, что при раскрытии скобок данный многочлен будет иметь одинаковые коэффициенты везде, где у исходного были одинаковые коэффициенты)
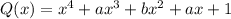(симметричный многочлен)
Умножим его на (x+1) и найдем a и b
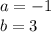
Тогда
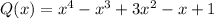
Тогда, чтобы найти корни многочлена 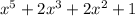нужно найти корни 
, т.е. решить уравнение
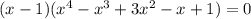
Тогда или х = - 1 или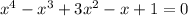 
Решим это уравнение
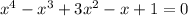
так как х=0 не корень, то мы можем поделить на x² обе части уравнения
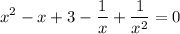
Тогда сделаем замену
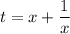
Тогда
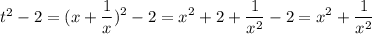
Преобразуем исходный многочлен
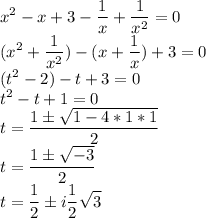
Тогда сделаем обратную замену и решим для всех вариантов для t
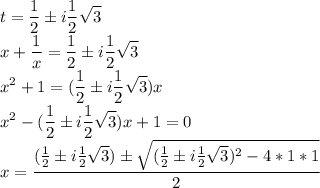
Тогда есть 2 варианта:
1)
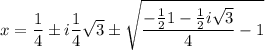
2)
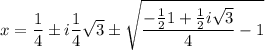
Тогда корни нашего исходного многочлена это
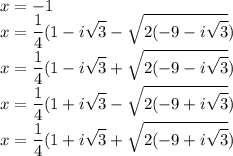
1)а=2³×3×5 и b=2×3×5²
b=2×3×5×5
а=2×2×2×3×5
НОК(а;b)=2×3×5×5×2×2=600
2)с=2⁴×3²и d=2²×3²×⁵
d=2×2×3×3×5
с=2 × 2 x 2 x 2 x 3 x 3
НОК(с;d)=2 x 2 x 3 x 3 x 5 x 2 x 2 =720
3)е=2³×3×7 и f=2²×3²×7
f=2 x 2 x 3 x 3 x 7
е=2 x 2 x 2 x 3 x 7
НОК(е;f)=2 x 2 x 3 x 3 x 7 x 2=504
4)m=2²×3² и n=3³×5
m= 2 x 2 x 3 x 3 x 3
n=3 x 3 x 3 x 5
НОК(m;n)=2 умножить на 2 x 3 X 3 x 3 x 5
5)р=3×3²×11 и t=2³×3×11
t=2 х 2 х 2 х 3 х 11
р=2 х 3 х 3 х 11
НОК(р;t)=2 х 2 х 2 х 3 х 11 х 3 = 792
6)х=2⁴×3×5 и у=2²×3×5²
у=2 x 2 x 3 x 5 x 5
х=2 x 2 x 2 x 2 x 3 x 5
НОК(х;у)=2 умножить на 2 x2× 3 x 5 x 5 x 2 x 2=1200
объяснение:разложим числа на простые множители.сначала запишем разложение на множители самого большого числа, затем меньшее число.чтобы определить НОК,необходимо недостающие множители добавить к множителем большего числа и перемножить их
строим график Ахмета - 8,16,24,32,40,48
строим график Самата - 12,24,36,48
Подчёркиваем совпадения, это и будет нашим ответом - 24,48.
ответ: 2 раза они будут вместе дежурить