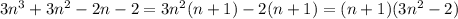
Поскольку число должно быть простым, то есть не должно раскладываться в произведение натуральных чисел, больших 1, одна из скобок равна 1. Но первая больше 1, значит, вторая равна 1:
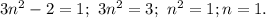
При этом первая скобка равна 2, и само число равно 2, то есть является простым.
ответ: n=1
№1.
а) 126 = 2 * 3 * 3 * 7
б) 84 = 2 * 2 * 3 * 7
№2.
Чтобы найти НОД нужно перемножить общие множители:
а) НОД (126; 84) = 2 * 3 * 7 = 42
Чтобы найти НОК, нужно к множителям бОльшего числа добавить недостающие множители и перемножить:
б) НОК (126; 84) = 2 * 3 * 3 * 7 * 2 = 252
№3.
Т.к. НОК (84; 126) = 42:
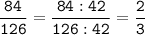
№4.
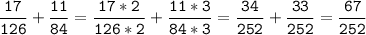
№5.
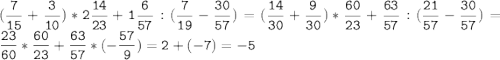
№6.
а) 105 = 3 * 5 * 7
б) 924 = 2 * 2 * 3 * 7 * 11
№7.
а) НОД (105; 924) = 3 * 7 = 21
б) НОК (105; 924) = 2 * 2 * 3 * 7 * 11 * 5 = 4620
№8.
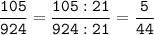
№9.
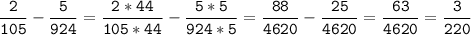
№10.
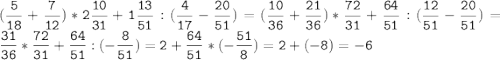
№11.
а) 630 = 2 * 3 * 3 * 5 * 7
б) 252 = 2 * 2 * 3 * 3 * 7
№12.
а) НОД (630; 252) = 2 * 3 * 3 * 7 = 126
б) НОК (630; 252) = 2 * 3 * 3 * 5 * 7 * 2 = 1260
№13.
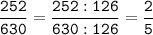
№14.
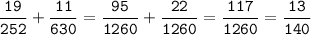
№15.
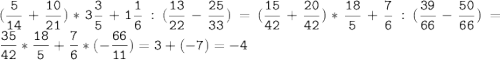
1. 5544 = 2 * 2 * 2 * 3 * 3 * 7 * 11
2. 504 = 2 * 2 * 2 * 3 * 3 * 7 756 = 2 * 2 * 3 * 3 * 3 * 7
НОД (504; 756) = 2 * 2 * 3 * 3 * 7 = 252 - наибольший общий делитель
НОК (504; 756) = 2 * 2 * 2 * 3 * 3 * 3 * 7 = 1512 - наименьшее общее кратное
3. а) 255 = 3 * 5 * 17 238 = 2 * 7 * 17
НОД (255; 238) = 17 - наибольший общий делитель
Числа 255 и 238 не взаимно простые, так как у них есть общий делитель
б) 392 = 2 * 2 * 2 * 7 * 7 675 = 3 * 3 * 3 * 5 * 5
Числа 392 и 675 не взаимно простые, так как у них нет общих делителей, кроме единицы.
4. Разность двух простых чисел может быть простым числом
Подробнее - на -
A=3n³+3n²-2n-2=3n²(n+1)-2(n+1) =(n+1)(3n²-2) , при n=1 A=2 (простое) , если n>1 , то n+1 ≥ 2 и 3n²-2 >1 ( так как n>1 ⇒n²>1⇒3n²>3 ⇒3n²-2 >1) ⇒ число А не может быть простым
А простое только при n=1