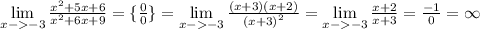
Пошаговое объяснение:
. (- 2,5 + 2 1/3) * (- 5 1/7) + 1 1/3 : (- 5,6) = 5/7
1) - 2,5 + 2 1/3 = - 2 5/10 + 2 1/3 = - 2 1/2 + 2 1/3 = - 2 3/6 + 2 2/6 = - 1/6
2) - 1/6 * (-5 1/7) = 1/6 * 36/7 = 6/7
3) 1 1/3 : (- 5,6) = 1 1/3 : (- 5 6/10) = - 1 1/3 : 5 3/5 = - 4/3 : 28/3 = - 4/3 * 3/28 = - 4/28 = - 1/7
4) 6/7 - 1/7 = 5/7
2. - 0,3x + 0,9 = - 4,2;
- 0,3x = - 4,2 - 0,9;
- 0,3 = - 5,1;
x = - 5,1 : (- 0,3);
x = 17.
ответ. 17.
3. - 0,25x + 0.8 = 1,3;
- 0,25x = 1,3 - 0,8;
- 0,25x = 0,5;
x = 0,5 : (- 0,25);
x = - 2.
ответ. - 2.
Пошаговое объяснение:
2sin²x - 3sinx + 1 = 0.
Это квадратное уравнение относительно переменной sinx.
Заменим основную переменную.
sinx = t, где -1 ≤ t ≤ 1, тогда sin²x = t².
Получим следующее квадратное уравнение:
2t² - 3t + 1 = 0.
Решим его используя дискриминант квадратного уравнения:
D = 32 - 4 • 2 • 1 = 9 - 8 = 1;
t1 = (3 + 1) / 4 = 1, удовлетворяет условию -1 ≤ t ≤ 1;
t2 = (3 - 1) / 4 = 1 / 2, удовлетворяет условию -1 ≤ t ≤ 1.
Делаем обратную замену переменной:
sinx = 1 или sinx = 1 / 2;
x1 = п/2 + 2пk, где k ∈ Z;
или:
x2 = п/6 + 2пk, где k ∈ Z;
x3 = 5п/6 + 2пk, где k ∈ Z.